Calculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
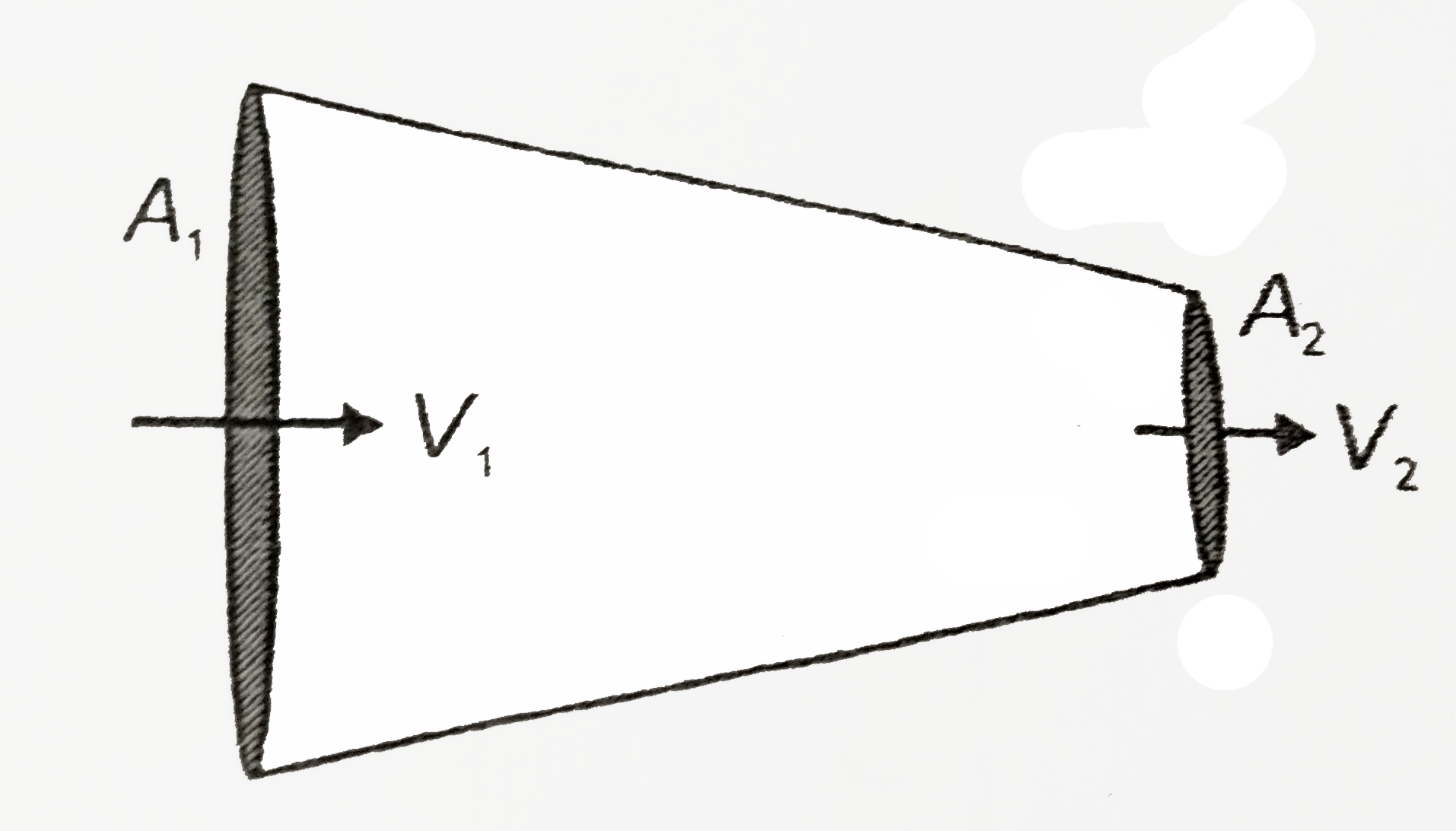
According to continuity equation,
A1V1=A2V2
⇒V2V1=A1A2=πr21πr22=r21r22
⇒V2V1=(r1r2)2=(0.100.02)2=52=25 ...(i)
and according to Bernoulli's equation
P1+12ρv21+ρgh1=P2+12ρv22+ρgh2
Here pipe is horizontal. So h1=h2
⇒P1+12ρv21+ρgh1=P2+12ρv22+ρgh1
⇒P1+12ρv21=P2+12ρv22
⇒12ρv22−12ρv21=P1−P2
⇒v22−v21=2(P1P2)ρ=2×101.20×103=201.20×103
⇒v22−v21=201200=2120=160=16.7×10−3 ...(ii)
Substituting the value of V2 from equation (i) in (ii)
(25V1)2−V21=16.7×10−3
⇒624V21=16.7×10−3
⇒v21=167×10−4624
⇒V1=√167624×10−2m/sec
So, rate of flow through the tube
R=A1V1=A2V2=π×(0.1)2×√167624×10−2
=π×√167624×10−4
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - TRY YOURSELF
41 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Calculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
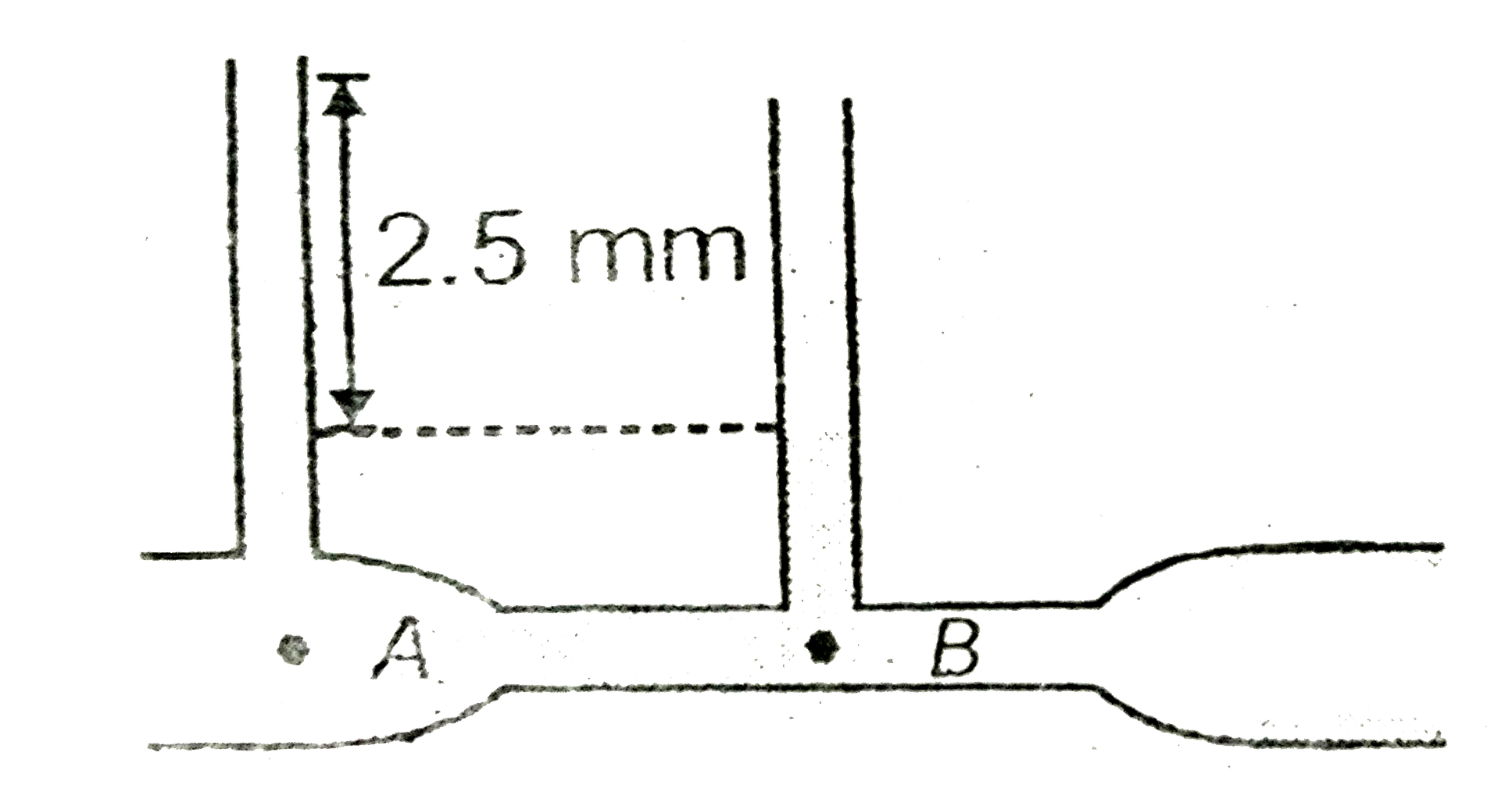
View Solution
Knowledge Check
An oil drop of diameter 4×10−6 m falls through air. iF the densities of the oil and air are 900 kg/m^(3)and1.293kgm3 respectively and the coefficient of viscosity of air is 2.0×10−5 Ns//m^(2), then the terminal velocity of oil drop will be
A0.2×10−4 m/sB2×10−4 m/sC4×10−4 m/sD8×10−4 m/s
Calculate the pH of 1.0×103 M solution of NaCI
View SolutionA wire of density 9×103kg/m3 is stretched between two clamps 1m apart and is stretched to an extension of 4.9×10−4m. Young's modulus of material is 9×1010N/m2.
View SolutionTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
View SolutionThe volume of a cuboid is 7.68m3 if its length = 3.2 m and height = 1.0 m find its breadth.
View SolutionTwo metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
View SolutionThe volume of a cuboid is 7.68m3if its length =3.2 m and height = 1.0 m : find its breadth.
View SolutionCalculate the speed of a transverse wave in a wire of 1.0mm2 cross-section under a tension of 0.98N. Density of the material of wire is 9.8×103kg/m3
View Solution
