Figure given here shows the variation of velocity of a particle with time.
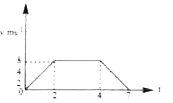
Find the following:
(i) Displacement during the time intervals.
(a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec
(ii) Accelerations at
(a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec.
(iii) Average acceleration
(a) between t = 0 to t = 4 sec.
(b) between t = 0 to t = 7 sec.
(iv) Average velocity during the motion.
The correct Answer is:i) a) 8m b) 16m c) 12m
ii) a) 4ma−2 b) 0 c) −8/3ms−2
iii) a) 2m/s2 b) 0 iv) 367ms−1
i) displacement = Area enclosed between v−t graph and time axis.
ii) Acceleration = slope of v−t curve
iii) Average acceleration = Total change in velocityTotal time
(iv) Average velocity = Total displacementTotal time
Similar Questions
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe position vector of a moving particle at't' sec is given by →r=3ˆi+4t2ˆj−t3ˆk . Its displacement during an interval of t = Is to 3 sec is
View SolutionThe current through a 4.6 H inductor is shown in the following graph. The induced emf during the time interval t = 5 milli - sec to 6 milli - sec will be
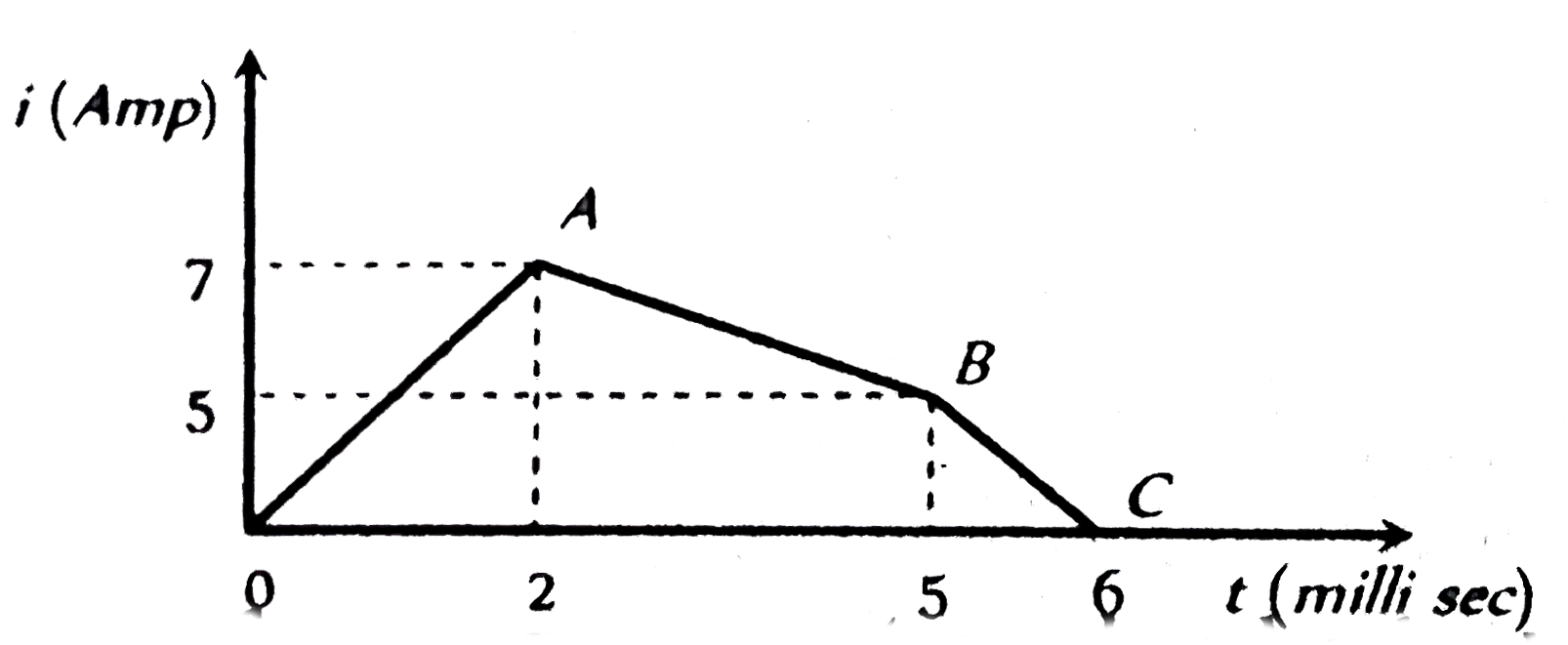 View Solution
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.View SolutionPosition of a particle at any instant is given by x=3t2+1 , where x is in m and t in sec. Its average velocity in the time interval t=2 sec to t=3 sec will be :
View SolutionA particle moves on a line according to the law s=at2+bt+c. If the displacement after 1 sec is 16 cm, the velocity after 2 sec is 24 cm/sec and acceleration is 8cm/sec2, then
View SolutionThe velocity (V) of a particle (in cm/s) is given in terms of time (t) in sec by the equation V=at+bc+t. The dimensions of a, b and c are
View SolutionIf v=(t+2)(t+3) then acceleration(i.edvdt) at t=1 sec.
View SolutionIf v=(t2−4t+105)m/s where t is in second. Find acceleration at t=1 sec.
View Solution
