The position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
To solve the problem step by step, we will follow the instructions given in the question.
Given:
The position of a particle is defined by the equation:
x(t)=3t2+5t3+7t
where x is in meters and t is in seconds.
(i) Displacement during the time interval t=1s to t=3s
1. Calculate x at t=3s:
x(3)=3(32)+5(33)+7(3)
=3(9)+5(27)+21
=27+135+21=183m
2. Calculate x at t=1s:
x(1)=3(12)+5(13)+7(1)
=3(1)+5(1)+7
=3+5+7=15m
3. Calculate displacement Δx:
Δx=x(3)−x(1)=183−15=168m
(ii) Average velocity during the time interval 0s to 5s
1. Calculate x at t=5s:
x(5)=3(52)+5(53)+7(5)
=3(25)+5(125)+35
=75+625+35=735m
2. Calculate x at t=0s:
x(0)=3(02)+5(03)+7(0)=0m
3. Calculate average velocity Vavg:
Vavg=ΔxΔt=x(5)−x(0)5−0=735−05=147m/s
(iii) Instantaneous velocity at t=0 and t=5
1. Find the expression for instantaneous velocity:
v(t)=dxdt=ddt(3t2+5t3+7t)=6t+15t2+7
2. Calculate v(0):
v(0)=6(0)+15(02)+7=7m/s
3. Calculate v(5):
v(5)=6(5)+15(52)+7
=30+15(25)+7=30+375+7=412m/s
(iv) Average acceleration during the time interval 0s to 5s
1. Calculate average acceleration Aavg:
Aavg=ΔvΔt=v(5)−v(0)5−0=412−75=4055=81m/s2
(v) Acceleration at t=0 and t=5
1. Find the expression for acceleration:
a(t)=dvdt=ddt(6t+15t2+7)=6+30t
2. Calculate a(0):
a(0)=6+30(0)=6m/s2
3. Calculate a(5):
a(5)=6+30(5)=6+150=156m/s2
Summary of Results:
- (i) Displacement from t=1s to t=3s: 168 m
- (ii) Average velocity from t=0s to t=5s: 147 m/s
- (iii) Instantaneous velocity at t=0s: 7 m/s, at t=5s: 412 m/s
- (iv) Average acceleration from t=0s to t=5s: 81 m/s²
- (v) Acceleration at t=0s: 6 m/s², at t=5s: 156 m/s²
The position of a particle is defined by the equation:
x(t)=3t2+5t3+7t
where x is in meters and t is in seconds.
x(3)=3(32)+5(33)+7(3)
=3(9)+5(27)+21
=27+135+21=183m
x(1)=3(12)+5(13)+7(1)
=3(1)+5(1)+7
=3+5+7=15m
Δx=x(3)−x(1)=183−15=168m
x(5)=3(52)+5(53)+7(5)
=3(25)+5(125)+35
=75+625+35=735m
x(0)=3(02)+5(03)+7(0)=0m
Vavg=ΔxΔt=x(5)−x(0)5−0=735−05=147m/s
v(t)=dxdt=ddt(3t2+5t3+7t)=6t+15t2+7
v(0)=6(0)+15(02)+7=7m/s
v(5)=6(5)+15(52)+7
=30+15(25)+7=30+375+7=412m/s
Aavg=ΔvΔt=v(5)−v(0)5−0=412−75=4055=81m/s2
a(t)=dvdt=ddt(6t+15t2+7)=6+30t
a(0)=6+30(0)=6m/s2
a(5)=6+30(5)=6+150=156m/s2
- (i) Displacement from t=1s to t=3s: 168 m
- (ii) Average velocity from t=0s to t=5s: 147 m/s
- (iii) Instantaneous velocity at t=0s: 7 m/s, at t=5s: 412 m/s
- (iv) Average acceleration from t=0s to t=5s: 81 m/s²
- (v) Acceleration at t=0s: 6 m/s², at t=5s: 156 m/s²
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Try Yourself
Explore 40 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - A)
Explore 50 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
The position x of a particle varies with time t according to the relation x=t3+3t2+2t. Find the velocity and acceleration as functions of time.
View SolutionThe position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and t = 1 s.
View SolutionAn object moves along x-axis such that its position varies with time according to the relation x=50t−5t2
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
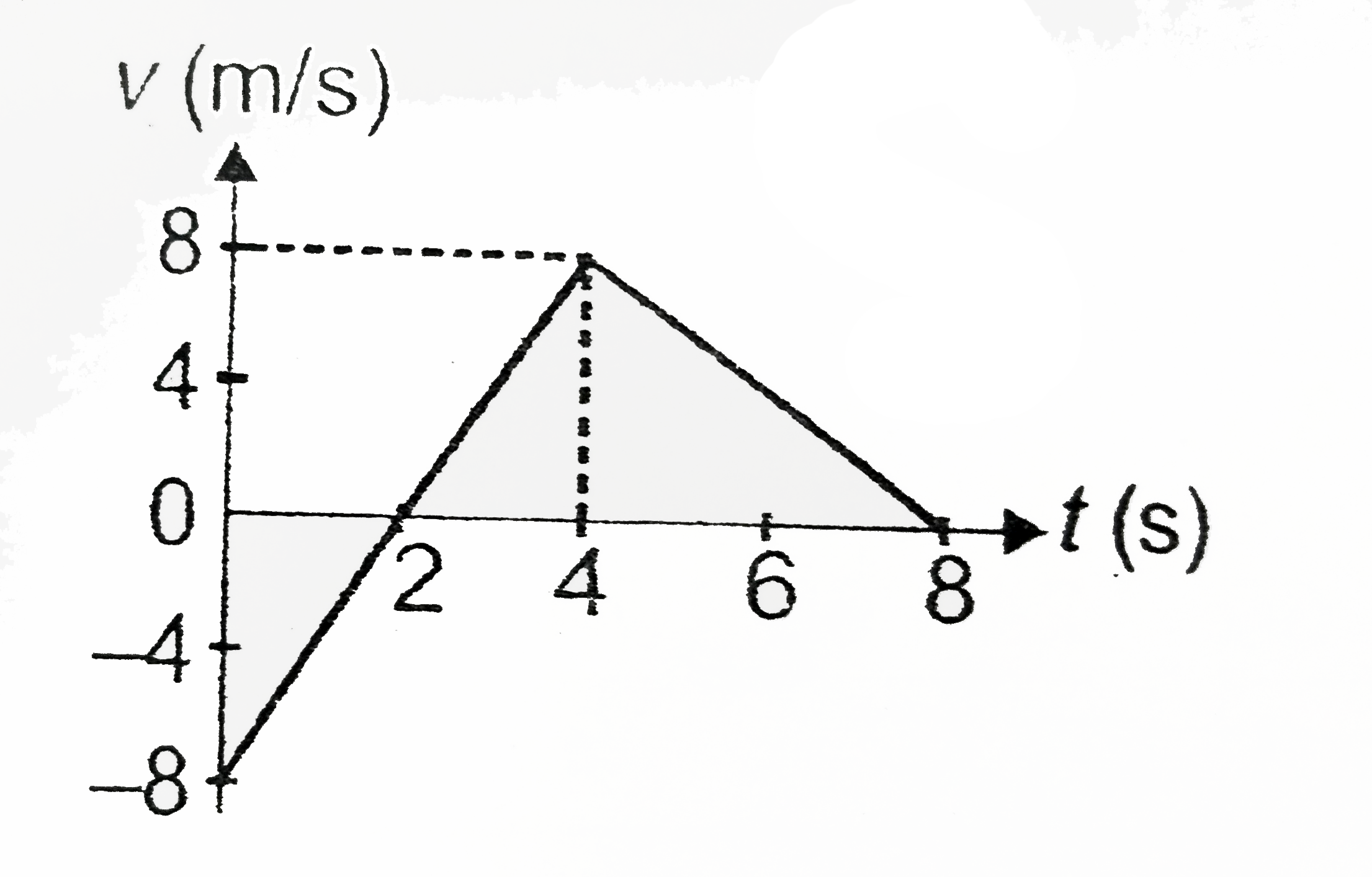
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
View SolutionThe position of a particle is given by the equation f(t)=t3−6t2+9t where t is measured in second and s in meter. Find the acceleration at time t. What is the acceleration at 4 s?
View SolutionPosition of a particle at any instant is given by x=3t2+1 , where x is in m and t in sec. Its average velocity in the time interval t=2 sec to t=3 sec will be :
View SolutionIf the particle is moving along a straight line given by the relation x=2−3t+4t3 where s is in cms., and t in sec. Its average velocity during the third sec is
View SolutionThe flux of magnetic field through a closed conducting loop of resistance 0.4Ω changes with time according to the equation Φ=0.20t2+0.40t+0.60 where t is time in seconds.Find (i)the induced emf at t=2s.(ii)the average induced emf in t=0 to t=5s.(iii)charge passed through the loop in t=0 to t=5s (iv)average current.In time interval t=0 to t=5s (v) heat produced in t=0 to t=5s
View SolutionA particle is moving in a straight line. Its displacement at any instant t is given by x=10t+15t3, where x is in meters and t is in seconds. Find
(i) the average acceleration in the intervasl t = 0 to t = 2s and
(ii) instantaneous acceleration at t = 2 s.
View SolutionThe displacement of a body of mass 2kg varies with time t as S=t2+2t, where S is in seconds. The work done by all the forces acting on the body during the time interval t=2s to t=4s is
View Solution