A particle moves according to the law x=rcos(pi)t/(2) The distance covered by it in the time interval between t=0 to t=3s is
Comparing the given equation with x=acosωt
⇒ω=π2 2πT=π2⇒T=4 sec
The given time t=3 sc is really 3T4
At time t=0 particle at x=a (at extreme position)
and at t=3 sec =3T4 it will be at mean position x=0
∴ distance covered wil be 3a.
Similar Questions
Knowledge Check
The speed-time graph of a particle moving along a fixed direction as shown in the figure. The distance traversed by the particle between t = 0 s to t = 10 s is
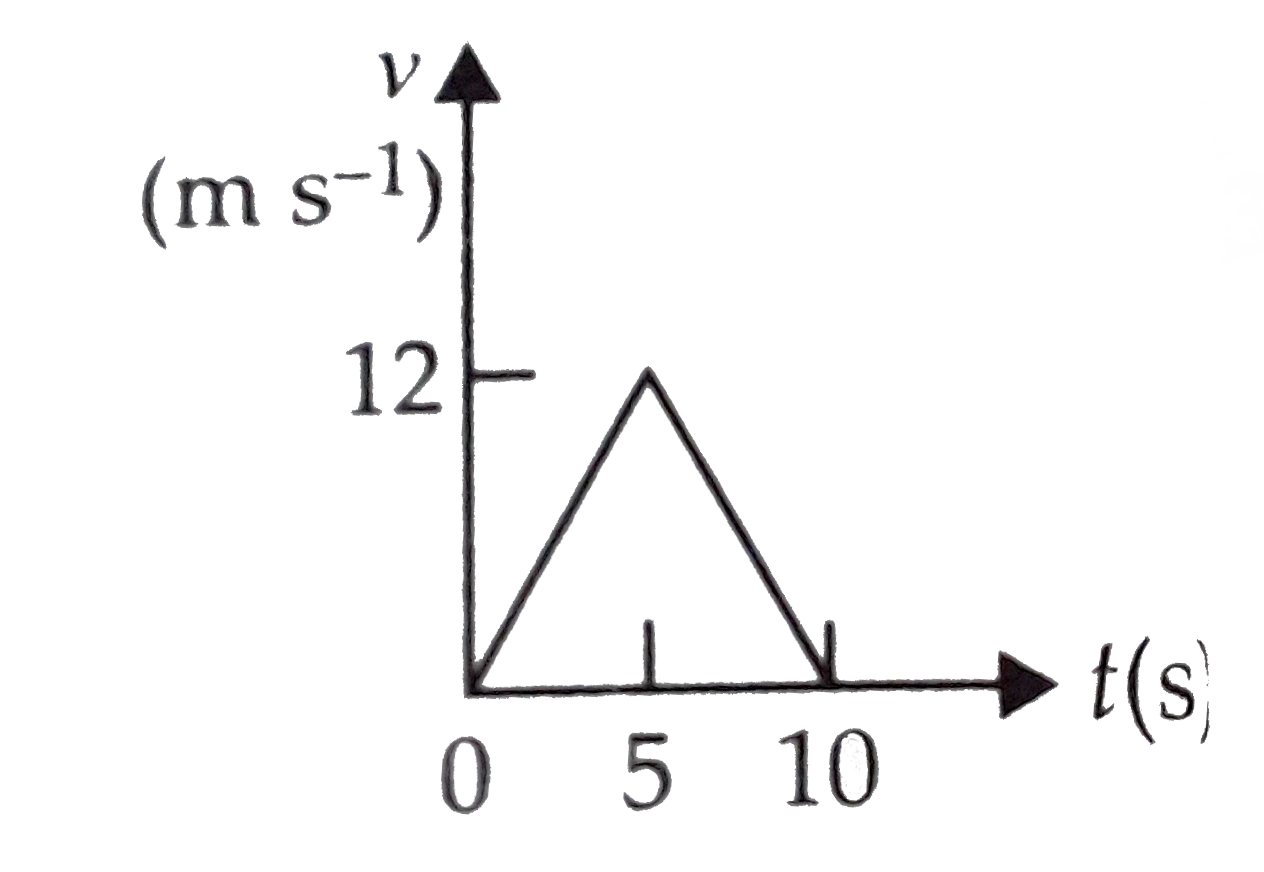A20 mB40 mC60 mD80 m
The diagram shows the displacement - time graph for a particle moving in a straight line. The distance (in m) coverted by the particle in the time interval t=0 to t=5s is
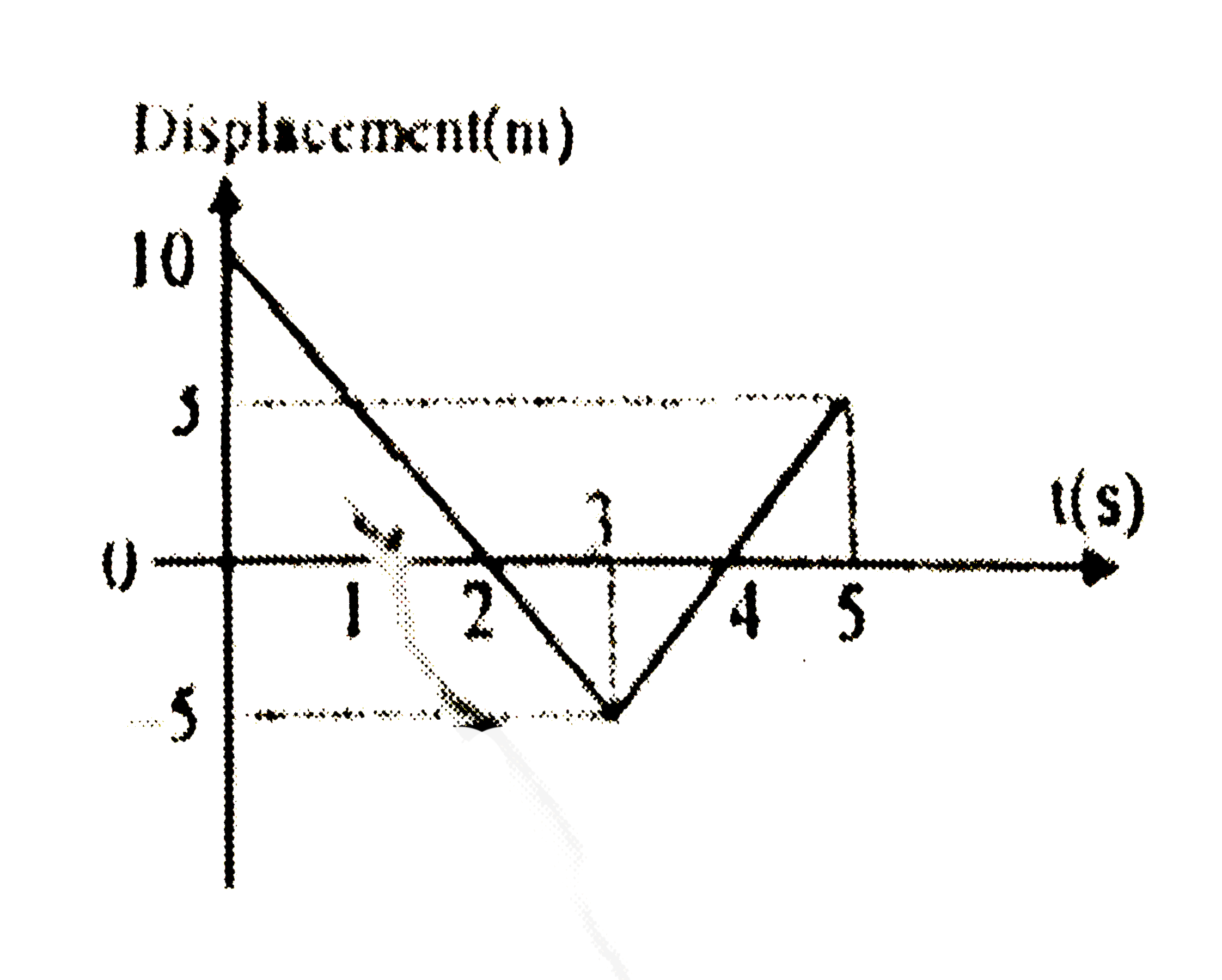
View SolutionIf a particle moves according to the law s=6t2−t32, then the time at which it is momentarily at rest is
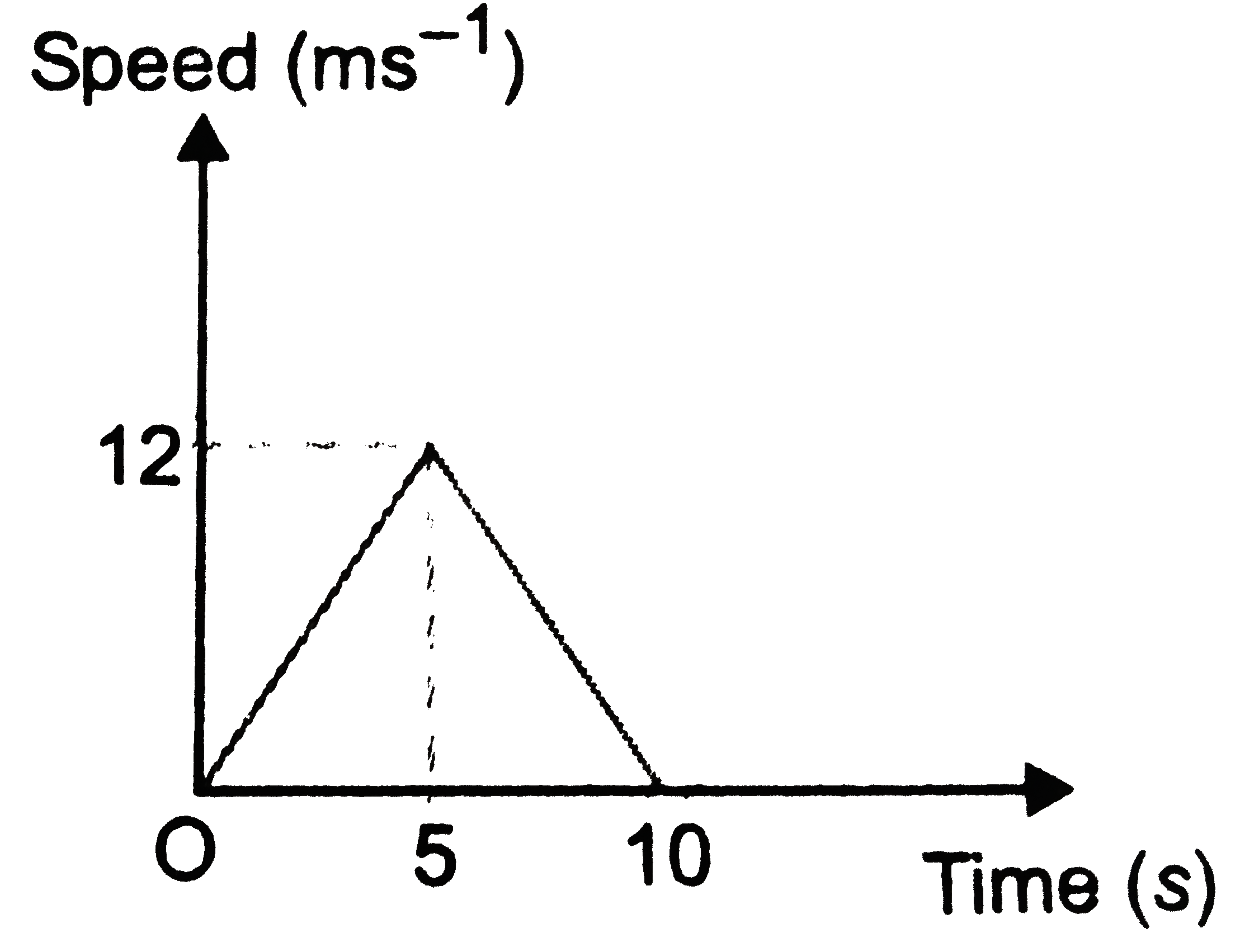
View SolutionThe speed verses time graph for a particle is shown in the figure. The distance travelled (in m) by the particle during the time interval t = 0 to t = 5 s will be __________
View SolutionA particle moves in x−y plane according to the law x=4sin6tandy=4(1−cos6t). The distance traversed by the particle in 4 second is (x&y are in meters)
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionThe speed-time graph of a particle moving along a fixed direction is shown in the Fig. The distance traversed by the particle between (a) t=0s→10s .
.
what is the average speed of the particle over the intervals?
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
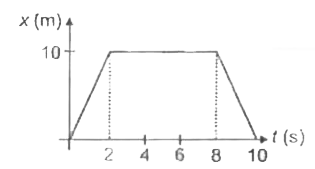
View Solution