In Cavendish's experiment, let each small mass be 20g and each large mass be 5kg. The rod connecting the small massess is 50 cm long, while the small and the large speres are separated by 10.0 cm. The torsion constant is and the resulting angular deflection is . Calculating the value of universal gravitational constant G from this data.
To calculate the value of the universal gravitational constant G using the data provided from Cavendish's experiment, we will follow these steps:
Step 1: Convert the Masses and Measurements to SI Units
- Small mass m=20g=0.02kg
- Large mass M=5kg
- Length of the rod l=50cm=0.5m
- Separation between small and large masses r=10cm=0.1m
- Angular deflection θ=0.4∘
Step 2: Convert Angular Deflection to Radians
To convert degrees to radians, we use the formula:
θ(radians)=θ(degrees)×π180
Calculating:
θ=0.4×π180≈0.007radians
Step 3: Use the Formula for Universal Gravitational Constant G
The formula for G in the context of Cavendish's experiment is:
G=k⋅θ⋅r2M⋅m⋅l
Where:
- k=4.8×10−8kg m2/s2 (torsion constant)
- θ=0.007radians
- r=0.1m
- M=5kg
- m=0.02kg
- l=0.5m
Step 4: Substitute the Values into the Formula
Substituting the values into the formula:
G=(4.8×10−8)⋅(0.007)⋅(0.1)2(5)⋅(0.02)⋅(0.5)
Step 5: Calculate the Numerator and Denominator
Calculating the numerator:
Numerator=4.8×10−8⋅0.007⋅0.01=3.36×10−12
Calculating the denominator:
Denominator=5⋅0.02⋅0.5=0.05
Step 6: Final Calculation of G
Now, calculate G:
G=3.36×10−120.05=6.72×10−11N m2/kg2
Final Answer
Thus, the value of the universal gravitational constant G is:
G≈6.72×10−11N m2/kg2
---
- Small mass m=20g=0.02kg
- Large mass M=5kg
- Length of the rod l=50cm=0.5m
- Separation between small and large masses r=10cm=0.1m
- Angular deflection θ=0.4∘
To convert degrees to radians, we use the formula:
θ(radians)=θ(degrees)×π180
Calculating:
θ=0.4×π180≈0.007radians
The formula for G in the context of Cavendish's experiment is:
G=k⋅θ⋅r2M⋅m⋅l
Where:
- k=4.8×10−8kg m2/s2 (torsion constant)
- θ=0.007radians
- r=0.1m
- M=5kg
- m=0.02kg
- l=0.5m
Substituting the values into the formula:
G=(4.8×10−8)⋅(0.007)⋅(0.1)2(5)⋅(0.02)⋅(0.5)
Calculating the numerator:
Numerator=4.8×10−8⋅0.007⋅0.01=3.36×10−12
Denominator=5⋅0.02⋅0.5=0.05
Now, calculate G:
G=3.36×10−120.05=6.72×10−11N m2/kg2
Thus, the value of the universal gravitational constant G is:
G≈6.72×10−11N m2/kg2
Similar Questions
A mass of 20kg is attached to one end of a steel wire 50cm long and is rotated in a horizontal circle. The area of cross-section of the wrie is 10−6m2 and the breaking stress for it is 4.8×107Pa. Calculate the maximum velocity with which the mass can be rotated.
View SolutionSilver crystallizes in fcc lattic. If the edge length of the cell is 4.07×10−8cm and density is 10.5gcm−3. Calculate the atomic mass of silver.
View Solution
Knowledge Check
The value of universal gravitational constant G=6.67×10−11Nm2kg−2. The value of G in units of g−1cm3s−2 is
A6.67×10−8B6.67×10−7C6.67×10−9D6.67×10−10A spring balance has a scale that reads from 0 to 50 kg. the length of the scale is 20 cm. a block of mass m is suspended from this balance, when displaced and released, it oscillates with a period 0.5 s. the value of m is (Take g=10ms−2)
A8 kgB12 kgC16 kgD20 kg
Silver crystallizes in fcc lattic. If the edge length of the cell is 4.07×10−8cm and density is 10.5gcm−3. Calculate the atomic mass of silver.
View SolutionCalculate the gravitational force of attraction between two bodies of masses 40 kg and 80 kg separated by a distance 15 m. Take G=6.7×10−11Nm2kg−2
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of +4.0×10−5C. They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View SolutionFour solid sphereas each of diameter √5cm and mass 0.5kg are placed with their centres at the corners of a square of side 4cm. The moment of inertia of the system about the diagonal of the square is N×10−4kg−m2, the N is -
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
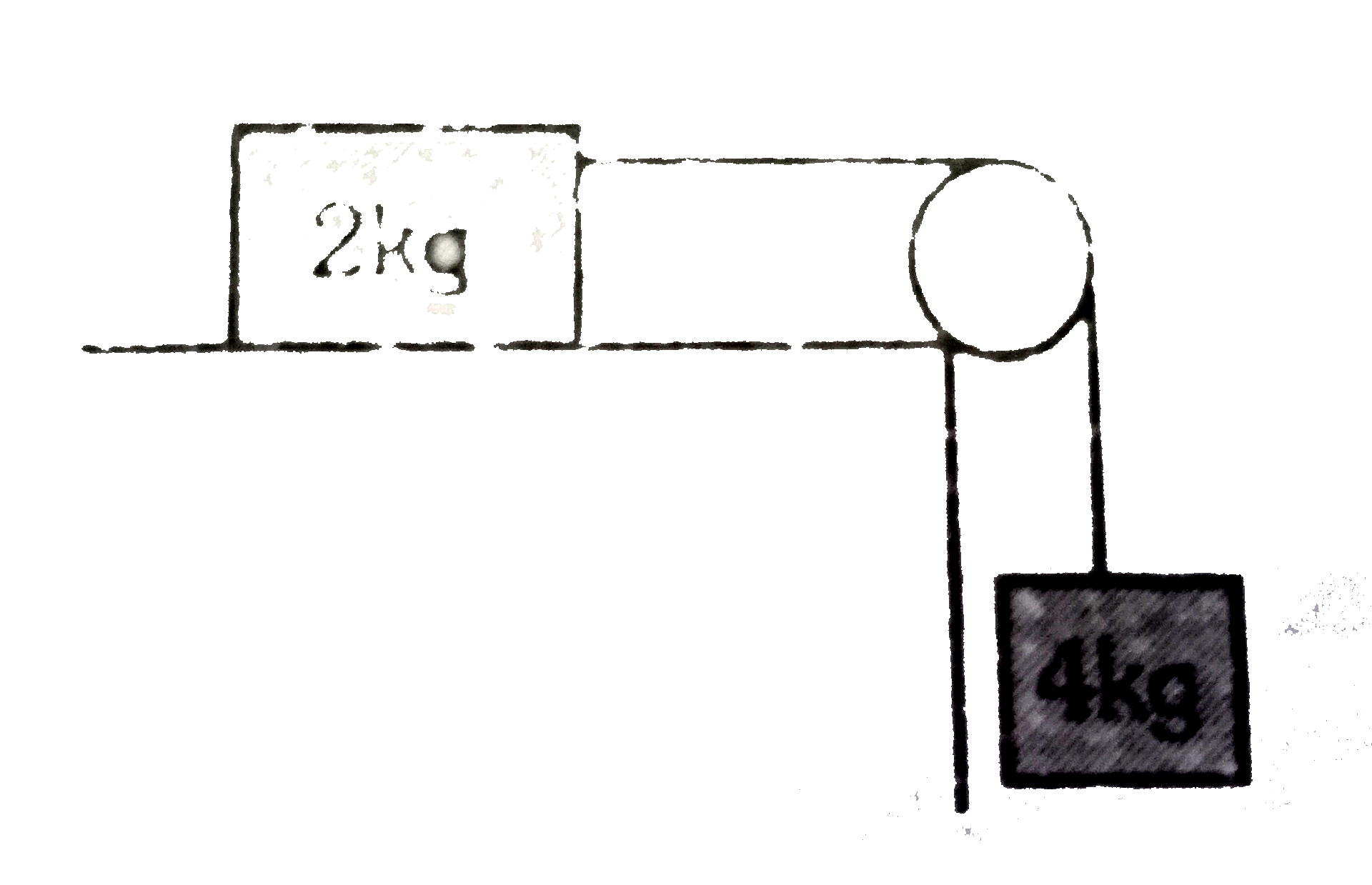
View Solution