Two bodies of masses are separated by certain distance. If is the force on due to is the force on due to then
both 1 & 3
The correct Answer is:D
To solve the problem, we need to analyze the forces acting between two masses m1 and m2 that are separated by a distance r. The forces →F12 and →F21 represent the gravitational force exerted by mass m2 on mass m1 and the gravitational force exerted by mass m1 on mass m2, respectively.
1. Understanding Newton's Third Law: According to Newton's Third Law of Motion, for every action, there is an equal and opposite reaction. This means that the force exerted by m2 on m1 is equal in magnitude and opposite in direction to the force exerted by m1 on m2.
→F12=−→F21
2. Magnitude of Forces: The magnitudes of the forces can be expressed as:
|→F12|=|→F21|
This indicates that the forces are equal in magnitude.
3. Vector Representation: If we consider the direction of the forces, we can represent them as:
- Let →F12 be directed towards m2 (the force on m1 due to m2).
- Let →F21 be directed towards m1 (the force on m2 due to m1).
Therefore, we can write:
→F12=−→F21
4. Conclusion: From the above analysis, we can conclude that:
- The forces are equal in magnitude but opposite in direction.
- This confirms that →F12 and →F21 are related by the equation →F12=−→F21.
Final Answer:
Both statements |→F12|=|→F21| and →F12=−→F21 are true.
|→F12|=|→F21|
- Let →F12 be directed towards m2 (the force on m1 due to m2).
- Let →F21 be directed towards m1 (the force on m2 due to m1).
- The forces are equal in magnitude but opposite in direction.
- This confirms that →F12 and →F21 are related by the equation →F12=−→F21.
Both statements |→F12|=|→F21| and →F12=−→F21 are true.
Similar Questions
Two particles of masses m1 and m2 (m1>m2) are separated by a distance d. The shift in the centre of mass when the two particles are interchanged.
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionGravitational force between a point mass m and M separated by a distance is F. Now if a point mass 2m is placed next to m is contact with it. The force on M due to m and the total force on M are
View SolutionGravitational force between two point masses m and M separated by a distance r is F. Now if a point mass 3m is placed next to m, what will be the (a) force on M due to m, (b) total force on M?
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.
View SolutionTwo bodies with masses m1kgandm2kg have equal kinetic energies. If p1andP2 are their respective momenta, then p1/P2 is equal to :
View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
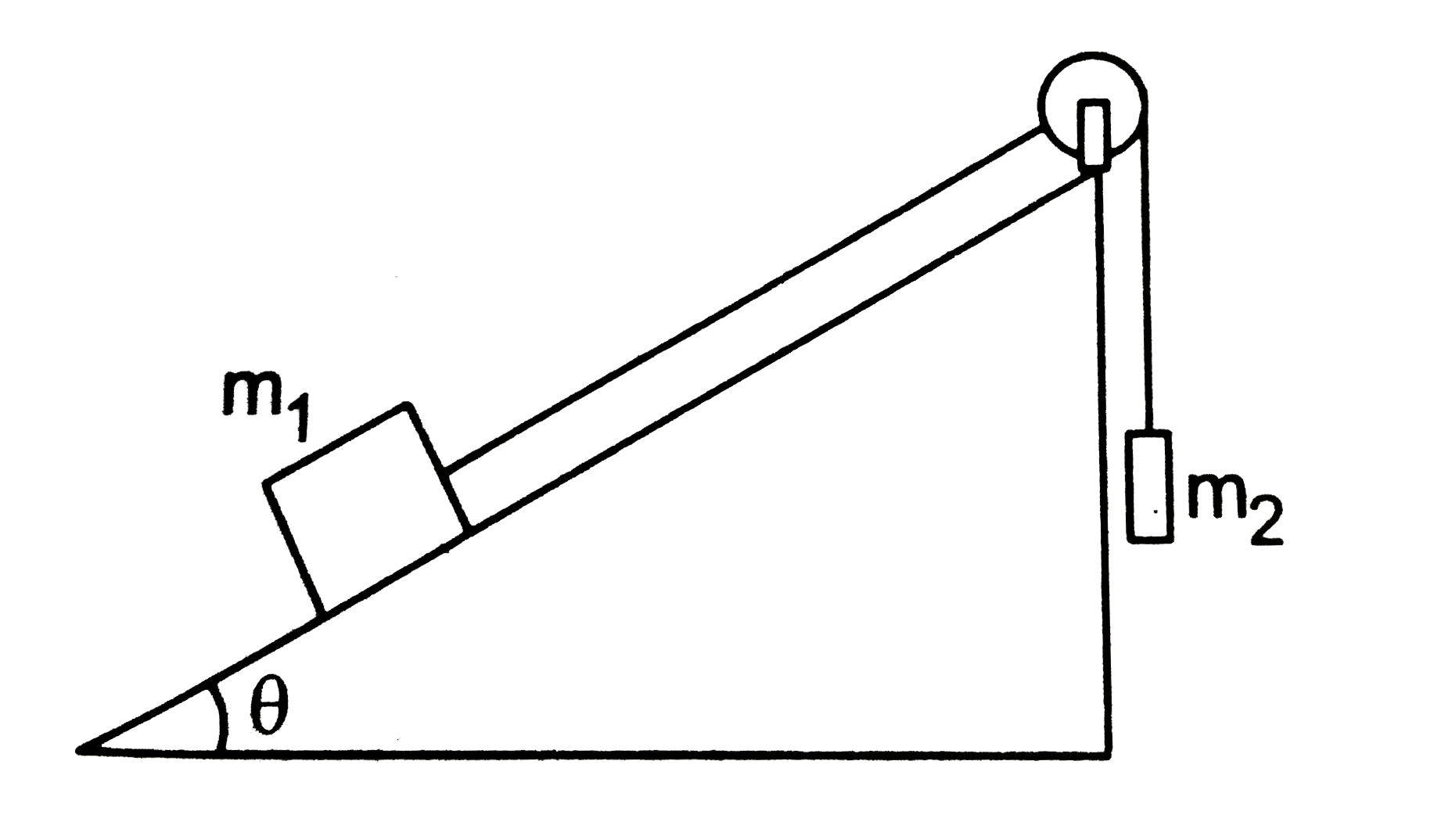
View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

View SolutionTwo blocks of masses m1 and m2 are connected to each other with the help of a spring. If pushing force F is given to the mass m1 providing acceleration a to it, then acceleration of m2 is
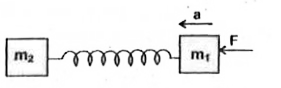
View SolutionAssertion : Two bodies of unequal masses m1andm2 are dropped from the same height. If the resistance offered by air to the motion of both bodies is the same, the bodies will reach the earth at the same time.
Reason : For equal air resistance, acceleration of fall of masses m1andm2 will be different.
View Solution
