Three particle each of mass m, are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?
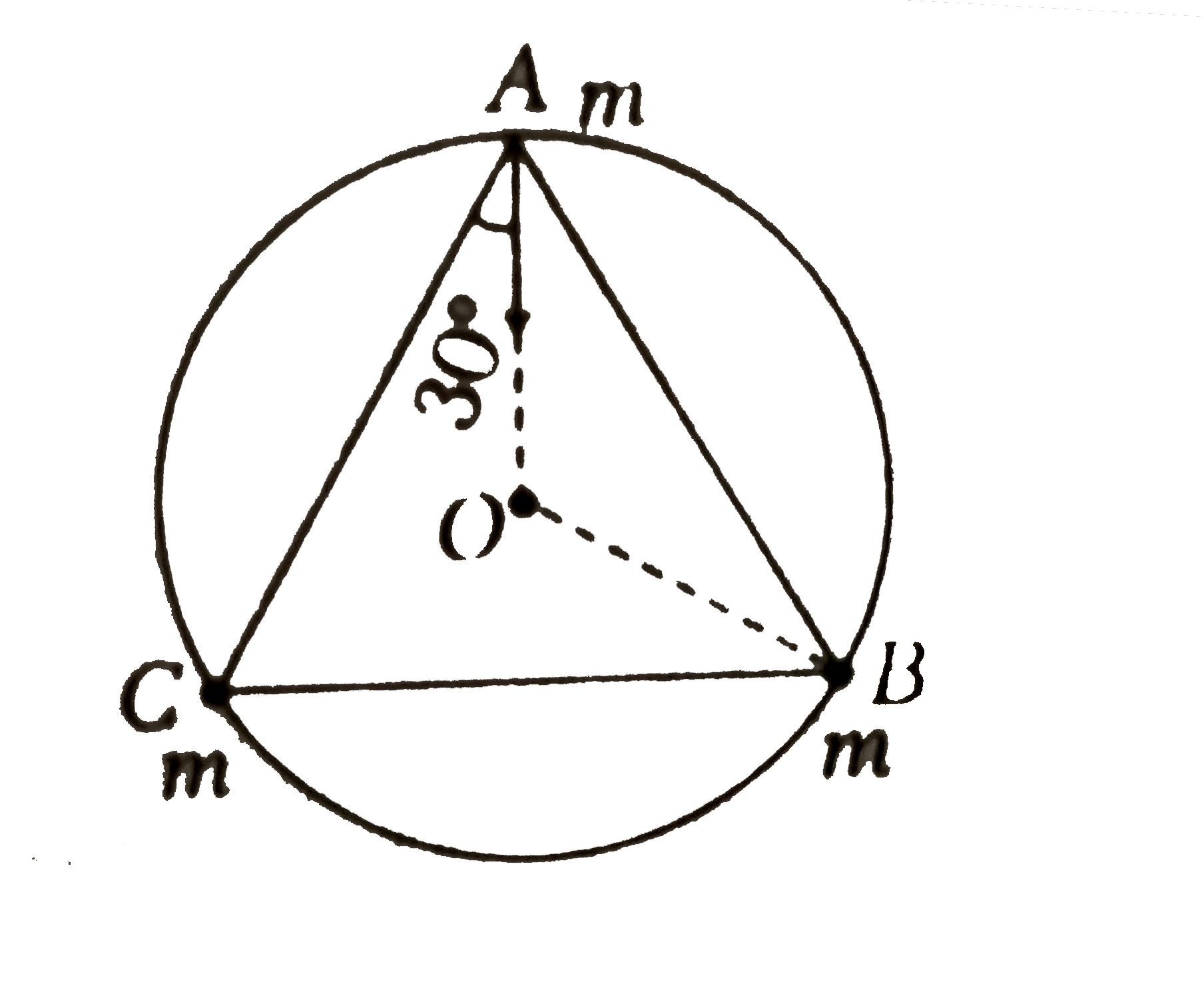

The force of attraction on body C due to bodies at A and B are
F1=Gm2a2 along CAandF2=Gm2a2 along CB
The resultant force on the body at C is
F=√F21+F22+2F1F2cos60∘=√3F1=√3Gm2a2
(∴F1=F2=Gm2a2)
The resultant force acting along CD, Here OC = a√3
When each body is describing a circular orbit with centre of orbit at O, the force F provides the required centripetal force. The radius of the circular orbit is OC = a/ √3 , If V is the speed of the body in circular orbit, then Centripetal force = resultant gravitational force
mV2a/√3=√3Gm2a2 or V=√Gma
Similar Questions
Three particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
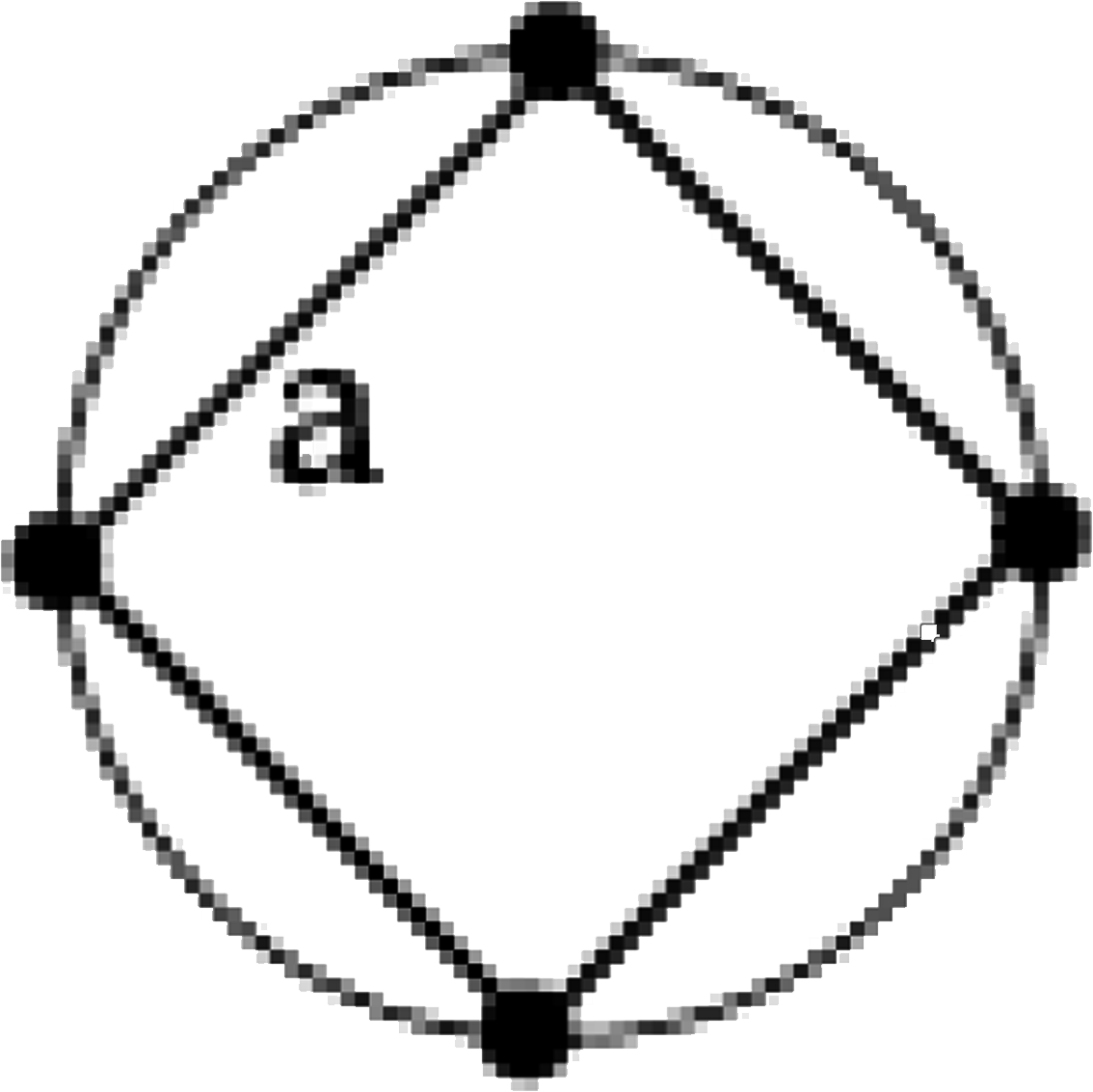
View SolutionFour identical particles of mass M are located at the corners of a square of side 'a'. What should be their speed if each of them revolves under the influence of others' gravitational field in a circular orbit circumscribing the square?
View Solution
Knowledge Check
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2DzeroThree particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
Three particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?
View SolutionThree identical point objects each of mass m are placed at the vertices of an equilateral triange of side l. What is the gravitational potential at the centre of the equilateral triangle due to the point masses?
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View Solution