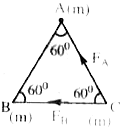
Three particles of identical masses .m. are kept at the vertices of an equilateral triangle of each side length.a.. Find the gravitational force of attraction on any one of the particles.Solution in Telugu
Let FA and FB be the forces due to the masses at A and B on the mass at C.
Here FA=FB
Hence the Resultant force on the mass at C
F=2FAcosθ/2=2.Gm2a2cos30∘
=2×Gm2a2×√32=√3Gm2a2
Topper's Solved these Questions
- GRAVITATIONBook:AAKASH SERIESChapter:GRAVITATIONExercise:Exercise-I
Explore 124 Videos
- GRAVITATIONBook:AAKASH SERIESChapter:GRAVITATIONExercise:Exercise-II
Explore 78 Videos
- GAUSS.S LAW Book:AAKASH SERIESChapter:GAUSS.S LAW Exercise:PROBLEMS (LEVEL - II)
Explore 12 Videos
- GRAVITATIONALBook:AAKASH SERIESChapter:GRAVITATIONALExercise:EXERCISE -3
Explore 154 Videos
Similar Questions
According to Kepler, the period of revolution of a planet (T) and its mean distance from the Sun (R) are related by the equation
View SolutionA planet revolves round the sun in an elliptical orbit of minor and major axes x and y respectively . Then the time period of revolution is proportional to
View SolutionA charge q is placed at the centre of the open end of a cyclindrical vessel. Find the flux of the electric through the surface of the vessel.
View SolutionA satellite takes 1/8 years to move round the earth in its permissible orbit of radius R. The period when it revolves round the earth in an orbit of radius '2R' is
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L . The gravitational field at the centre due to these particle is
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the (a) the mid point of a side (b) centre of the triangle
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThe gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
View SolutionThree particles each of mass m are placed at the three corners of an equilateral triangle of side L. A particle of mass M is kept at the midpoint of any one side. What is the force acting on M, due to this system of 3 particles ?
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a . The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions. Force acting on particle C , due to particle A and B
View SolutionThree particles of the same mass are kept at the vertices of an equilateral triangle. The mass of each particle is m and the length of an arm of the triangle is l. Due to the the mutual gravitational force of attraction, the particles revolve along the circumcircle of the triangle. Find the velocity of each particle.
View SolutionAt the vertices of an equilateral triangle of side a, three particles each of mass m are kept. Find the gravitational potential and the gravitational field at the centroid of the triangle.
View SolutionThree equal masses .m. are placed at the three vertices of an equilateral triangle of side a. Find the gravitational force exerted by this system on another particle of mass ‘m. placed a) at the mid point of a side and (b) at the centroid of the triangle.
View Solution

