An electric pump on the ground floor of a building taken 15 minutes to fill a tank of volume 30ms3 with water. If the tank is 40m above the ground and the efficiency of pump is 30% find the electira power consumed by the pump in filling the tank. [density of water = 103kg/m3
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the mass of water to be filled in the tank
The mass of water can be calculated using the formula:
mass=volume×density
Given:
- Volume of the tank, V=30m3
- Density of water, ρ=103kg/m3
So,
mass=30m3×103kg/m3=30000kg
Step 2: Calculate the work done to lift the water
The work done (W) against gravity can be calculated using the formula:
W=mgh
Where:
- m=30000kg (mass of water)
- g=9.8m/s2 (acceleration due to gravity)
- h=40m (height)
So,
W=30000kg×9.8m/s2×40m
W=11760000J
Step 3: Calculate the time taken in seconds
The time taken to fill the tank is given as 15 minutes. We need to convert this into seconds:
time=15minutes×60seconds/minute=900seconds
Step 4: Calculate the power output of the pump
The power output (P) can be calculated using the formula:
P=Wt
Where:
- W=11760000J
- t=900s
So,
P=11760000J900s
P=13066.67W (or 13.07kW)
Step 5: Calculate the input power considering efficiency
The efficiency (η) of the pump is given as 30%. The input power (Pinput) can be calculated using the formula:
Pinput=Poutputη
Where:
- Poutput=13066.67W
- η=0.30
So,
Pinput=13066.67W0.30
Pinput=43555.56W (or 43.56kW)
Final Answer:
The electric power consumed by the pump in filling the tank is approximately 43.56 kW.
---
The mass of water can be calculated using the formula:
mass=volume×density
- Volume of the tank, V=30m3
- Density of water, ρ=103kg/m3
mass=30m3×103kg/m3=30000kg
The work done (W) against gravity can be calculated using the formula:
W=mgh
- m=30000kg (mass of water)
- g=9.8m/s2 (acceleration due to gravity)
- h=40m (height)
W=30000kg×9.8m/s2×40m
W=11760000J
The time taken to fill the tank is given as 15 minutes. We need to convert this into seconds:
time=15minutes×60seconds/minute=900seconds
The power output (P) can be calculated using the formula:
P=Wt
- W=11760000J
- t=900s
P=11760000J900s
P=13066.67W (or 13.07kW)
The efficiency (η) of the pump is given as 30%. The input power (Pinput) can be calculated using the formula:
Pinput=Poutputη
- Poutput=13066.67W
- η=0.30
Pinput=13066.67W0.30
Pinput=43555.56W (or 43.56kW)
The electric power consumed by the pump in filling the tank is approximately 43.56 kW.
Similar Questions
A pump on the ground floor of a building can pump of water to fill a tank of volume 30ms3 in 15min. If the tank is 40m above the ground and the efficiency of the pump is 30% , how much electric power is consumed by the pump? (Takeg=10ms2)
View SolutionA pump on the ground floor of a building can pump up water to fill a tank of volume 30m3 in 15 min. If the tank is 60 m above the ground, and the efficiency of the pump is 40%, how much electric power is consumed by the pump?
(Take g=10ms−2)
View Solution
Knowledge Check
A pump on the ground floor of a building can pump of water to fill a tank of volume 30ms3 in 15min. If the tank is 40m above the ground and the efficiency of the pump is 30% , how much electric power is consumed by the pump? (Takeg=10ms2)
A36.5 kWB50 kWC52.5 kWD60.5 kW
An electric pump on the ground floor of a building taken 10 minute to fill a tank of 45m3 with water. The tank is 20m above the water level . If electric power consumed by the pump is 30kW then efficiency of the pump will be ( density of water is 1000kgm3)
View SolutionA water pump raises 50 litres of water through a height of 25 m in 5 .Calculate the power of the pump required . (Take g=10 N kg−1 and density of water =1000 kg m−3)
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
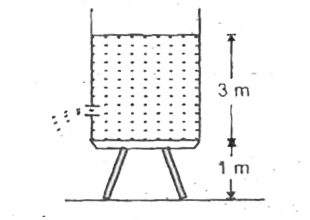
View SolutionThe pressure of water on the ground floor is 40,000 Pa and on the first floor is 10,000 Pa. Find the height of the first floor. (Take : density of water = 1000kg m−3,g=10m s−2 )
View SolutionA closed box of thin aluminium foil of volume 10 cc and mass 3 gm is completely filled with a liquid . It is now put into water and when it floats . It is just completely immersed . Find the density of the liquid filled inside the box ( density of water 103kg/m3)

View SolutionA rectangular water tank of base 11m×6m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
View Solution
