A disc of mass m and radius R has a concentric hole of radius r Find its moment of inertia about an axis through its centre and perpendicular to its plane?
Consider a ring of radius .x. and of thickness dx of the disc
The M.I. of the ring about a normal axis through its centre is dI=mπ(R2−r2)2πx.dx.x2
The total M.I of the disc is obtained by integrating the above expression. ∫dI=∫Rrmπ(R2−r2)2πx.dx.x2
on solving I=m2(R2+r2)
Similar Questions
A disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionA semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionA solid sphere of mass M, radius R and having moment of inertia about as axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains I. Then, radius of the disc will be.
View SolutionA circular disc of radius R and thickness R6 has moment of inertia about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
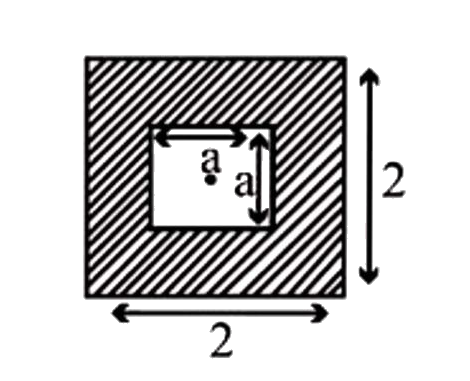
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
View Solution
