A particle traveling horizontally with speed u collides and sticks with a particle of equal mass hanging at rest at the end of a light inextensible string of length 21. If the string rotates through an angle of 60° before its velocity becomes zero, then u is
√4gl
√8gl
√2gl
√gl
The correct Answer is:B
To solve the problem step by step, we can follow these steps:
Step 1: Determine the vertical distance moved by the hanging mass.
The hanging mass moves through an angle of 60° when the string rotates. The vertical distance r moved by the mass can be calculated using the formula for vertical displacement in terms of the length of the string l:
r=2l−2lcos(60∘)
Since cos(60∘)=12:
r=2l−2l⋅12=2l−l=l
Step 2: Apply conservation of momentum.
Before the collision, the horizontal particle has momentum mu (where m is the mass and u is the speed). After the collision, both masses stick together and move with a common velocity v. By conservation of momentum:
mu=(m+m)v
This simplifies to:
mu=2mv
Dividing both sides by m:
u=2v⇒v=u2
Step 3: Apply conservation of energy.
The initial kinetic energy of the system is due to the moving particle, and the potential energy of the hanging mass is zero since it is at the lowest point. After the collision, the system has both kinetic and potential energy. The conservation of energy can be expressed as:
Initial Kinetic Energy+Initial Potential Energy=Final Kinetic Energy+Final Potential Energy
Initially, the potential energy is zero, and the kinetic energy is:
Initial K.E.=12mu2
At the highest point, the kinetic energy is:
Final K.E.=12(2m)v2=mv2
The potential energy at the highest point is:
Final P.E.=2mgr=2mgl
Setting the initial energy equal to the final energy:
12mu2=mv2+2mgl
Step 4: Substitute v and simplify.
Substituting v=u2:
12mu2=m(u2)2+2mgl
This simplifies to:
12mu2=mu24+2mgl
Multiplying through by 4 to eliminate the fractions:
2mu2=mu2+8mgl
Step 5: Solve for u2.
Rearranging gives:
2mu2−mu2=8mgl⇒mu2=8mgl
Dividing both sides by m:
u2=8gl
Step 6: Take the square root to find u.
Taking the square root:
u=√8gl
This is the final expression for u.
Final Answer:
u=√8gl
The hanging mass moves through an angle of 60° when the string rotates. The vertical distance r moved by the mass can be calculated using the formula for vertical displacement in terms of the length of the string l:
Before the collision, the horizontal particle has momentum mu (where m is the mass and u is the speed). After the collision, both masses stick together and move with a common velocity v. By conservation of momentum:
The initial kinetic energy of the system is due to the moving particle, and the potential energy of the hanging mass is zero since it is at the lowest point. After the collision, the system has both kinetic and potential energy. The conservation of energy can be expressed as:
Substituting v=u2:
Rearranging gives:
Taking the square root:
u=√8gl
Similar Questions
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision what could be minimum and the maximum value of u.
View SolutionA particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision what could be minimum and the maximum value of u.
View SolutionA particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision what could be minimum and the maximum value of u.
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. tension in the string
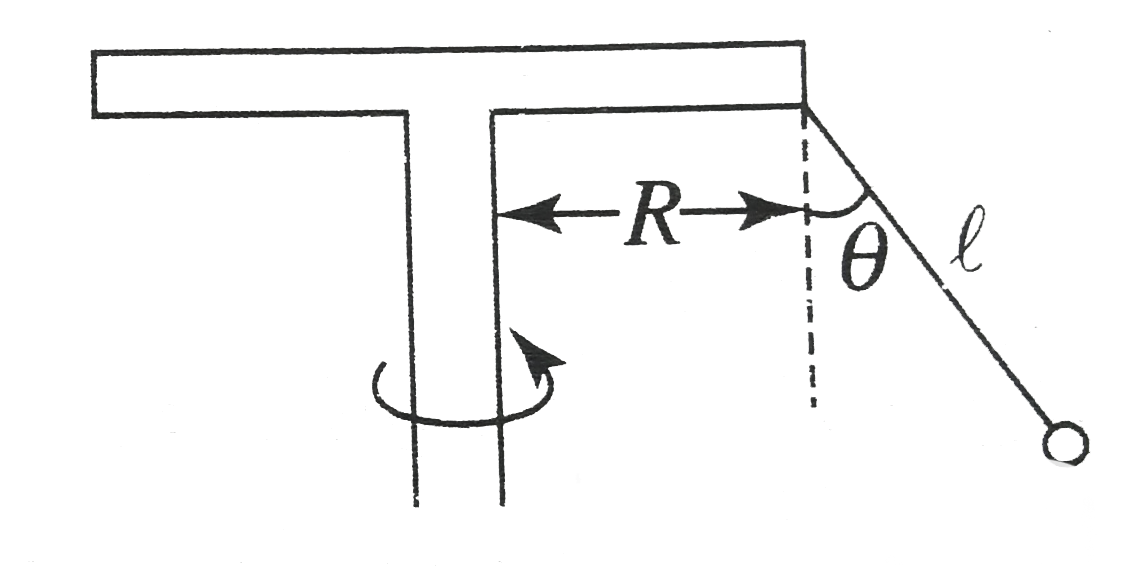
View SolutionIf a sphere of mass m moving with velocity u collides with another identical sphere at rest on a frictionless surface, then which of the following is correct ?
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
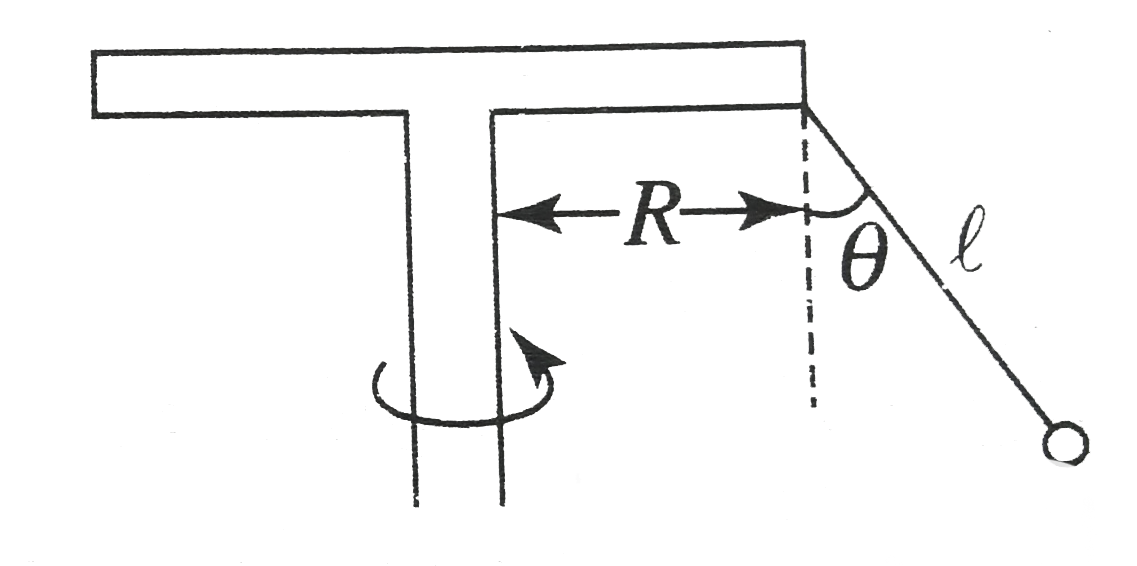
View Solution

