A block of mass .M. moving on the firctionless , horizontal surface collides with the spring of spring constant .k.. The other end of the spring is rigidly fixed to a vertical wall. If the spring is compressed by L, the maximum momentum of the block after collision is :
√MkL
kL22M
Zero
ML2k
The correct Answer is:A
To solve the problem, we need to apply the principle of conservation of mechanical energy. The block collides with the spring and compresses it, converting its kinetic energy into potential energy stored in the spring. Let's break down the solution step by step:
Step 1: Understand the conservation of energy
The total mechanical energy of the system remains constant if only conservative forces are acting. In this case, the kinetic energy of the block is converted into the potential energy of the spring.
Hint: Remember that the total mechanical energy is the sum of kinetic and potential energy.
Step 2: Write the expressions for kinetic and potential energy
- The initial kinetic energy (KE_initial) of the block is given by:
KEinitial=12Mv2
where v is the initial velocity of the block.
- The potential energy (PE) stored in the spring when compressed by a distance L is given by:
PE=12kL2
where k is the spring constant.
Hint: Identify the forms of energy involved in the collision.
Step 3: Apply conservation of energy
According to the conservation of energy:
KEinitial+PEinitial=KEfinal+PEfinal
Assuming the spring is uncompressed initially, we have:
12Mv2+0=0+12kL2
Hint: Set up the equation based on the initial and final states of the system.
Step 4: Rearrange the equation
From the above equation, we can rearrange it to find the initial velocity v:
12Mv2=12kL2
Cancelling the 12 from both sides gives:
Mv2=kL2
Now, solving for v2:
v2=kL2M
Hint: Isolate v2 to find the relationship with spring constant and compression.
Step 5: Find the maximum momentum
The momentum p of the block is given by:
p=Mv
Substituting the expression for v:
p=M√kL2M=L√Mk
Hint: Remember that momentum is mass times velocity.
Final Answer
Thus, the maximum momentum of the block after the collision is:
p=L√Mk
The total mechanical energy of the system remains constant if only conservative forces are acting. In this case, the kinetic energy of the block is converted into the potential energy of the spring.
- The initial kinetic energy (KE_initial) of the block is given by:
KEinitial=12Mv2
where v is the initial velocity of the block.
PE=12kL2
where k is the spring constant.
According to the conservation of energy:
KEinitial+PEinitial=KEfinal+PEfinal
Assuming the spring is uncompressed initially, we have:
12Mv2+0=0+12kL2
From the above equation, we can rearrange it to find the initial velocity v:
12Mv2=12kL2
Cancelling the 12 from both sides gives:
Mv2=kL2
Now, solving for v2:
v2=kL2M
The momentum p of the block is given by:
p=Mv
Substituting the expression for v:
p=M√kL2M=L√Mk
Thus, the maximum momentum of the block after the collision is:
p=L√Mk
Similar Questions
The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

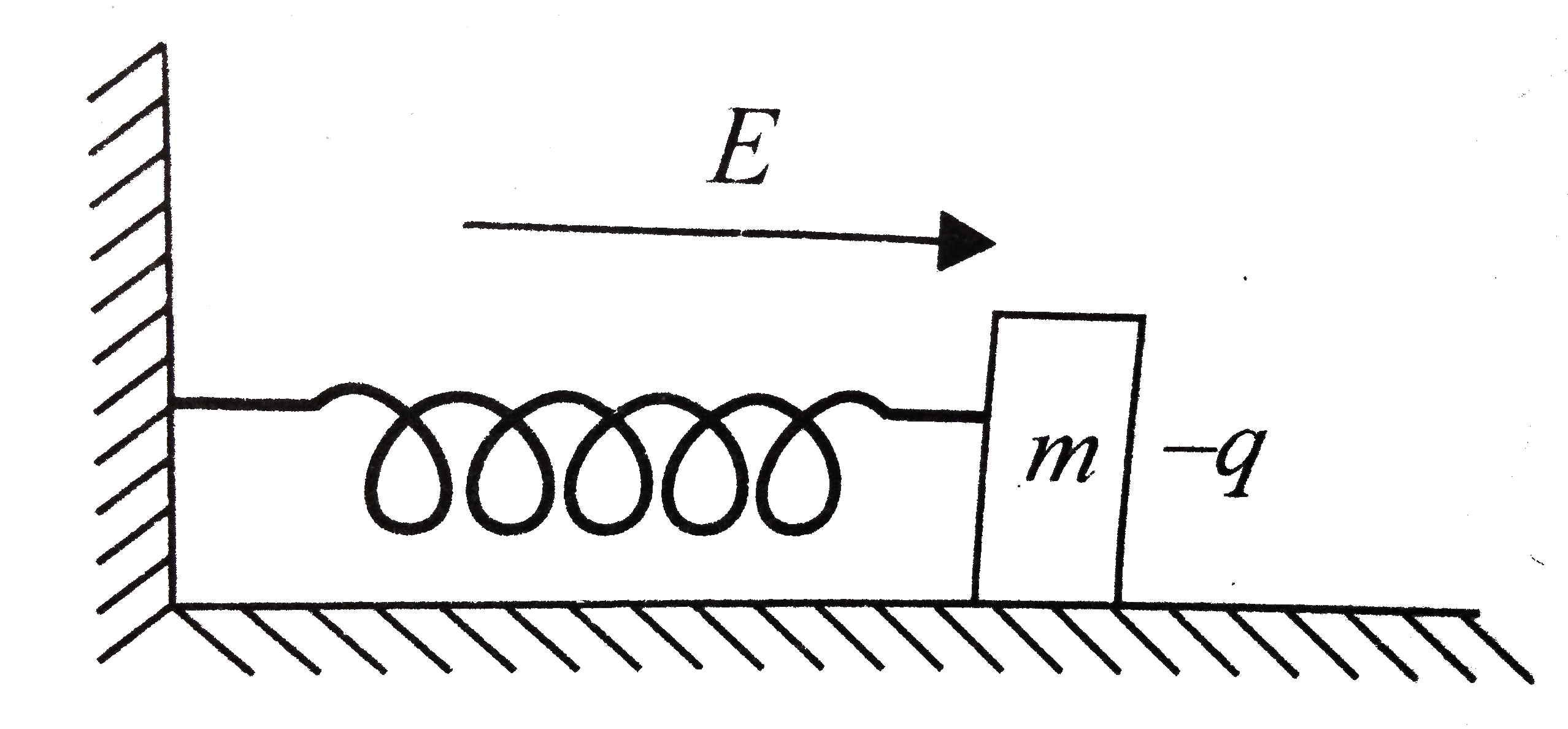
View SolutionA block of mass m containing a net negative chage −q is placed on a froctionless horizontal tabe and is connected to a wall through an unstreached spring of spring constant k. If the horizontal electric field E parallel to spring is switched on , then the maximum compression of the spring is
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution
