Particles of masses m1 and m2 are at a fixed distance apart . If the gravitational field strength at m1 and m2 are →I1 and →I2 respectively . Then ,
m1→I1+m2→I2=0
m1→I2+m2→I1=0
m1→I1−m2→I2=0
m1→I2−m2→I1=0
The correct Answer is:B
To solve the problem, we need to find the relationship between the gravitational field strengths at two masses m1 and m2, denoted as →I1 and →I2 respectively.
1. Understanding Gravitational Field Strength:
The gravitational field strength →I at a point due to a mass m is given by the formula:
→I=G⋅mr2^r
where G is the gravitational constant, r is the distance from the mass to the point where the field is being measured, and ^r is the unit vector pointing away from the mass.
2. Gravitational Field Strength at m1:
The gravitational field strength →I1 at mass m1 due to mass m2 is:
→I1=G⋅m2r2^r12
where ^r12 is the unit vector pointing from m2 to m1.
3. Gravitational Field Strength at m2:
Similarly, the gravitational field strength →I2 at mass m2 due to mass m1 is:
→I2=G⋅m1r2(−^r12)
Here, the negative sign indicates that the gravitational field due to m1 at m2 is directed towards m1.
4. Multiplying by Masses:
Now, we multiply both gravitational field strengths by their respective masses:
- For m1:
m1→I1=m1(G⋅m2r2^r12)=G⋅m1⋅m2r2^r12
- For m2:
m2→I2=m2(G⋅m1r2(−^r12))=−G⋅m1⋅m2r2^r12
5. Adding the Two Expressions:
Now, we add the two expressions:
m1→I1+m2→I2=G⋅m1⋅m2r2^r12−G⋅m1⋅m2r2^r12=0
6. Conclusion:
Therefore, we conclude that:
m1→I1+m2→I2=0
Final Answer:
The relation is:
m1→I1+m2→I2=0
The gravitational field strength →I at a point due to a mass m is given by the formula:
→I=G⋅mr2^r
where G is the gravitational constant, r is the distance from the mass to the point where the field is being measured, and ^r is the unit vector pointing away from the mass.
The gravitational field strength →I1 at mass m1 due to mass m2 is:
→I1=G⋅m2r2^r12
where ^r12 is the unit vector pointing from m2 to m1.
Similarly, the gravitational field strength →I2 at mass m2 due to mass m1 is:
→I2=G⋅m1r2(−^r12)
Here, the negative sign indicates that the gravitational field due to m1 at m2 is directed towards m1.
Now, we multiply both gravitational field strengths by their respective masses:
- For m1:
m1→I1=m1(G⋅m2r2^r12)=G⋅m1⋅m2r2^r12
- For m2:
m2→I2=m2(G⋅m1r2(−^r12))=−G⋅m1⋅m2r2^r12
Now, we add the two expressions:
m1→I1+m2→I2=G⋅m1⋅m2r2^r12−G⋅m1⋅m2r2^r12=0
Therefore, we conclude that:
m1→I1+m2→I2=0
The relation is:
m1→I1+m2→I2=0
Similar Questions
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
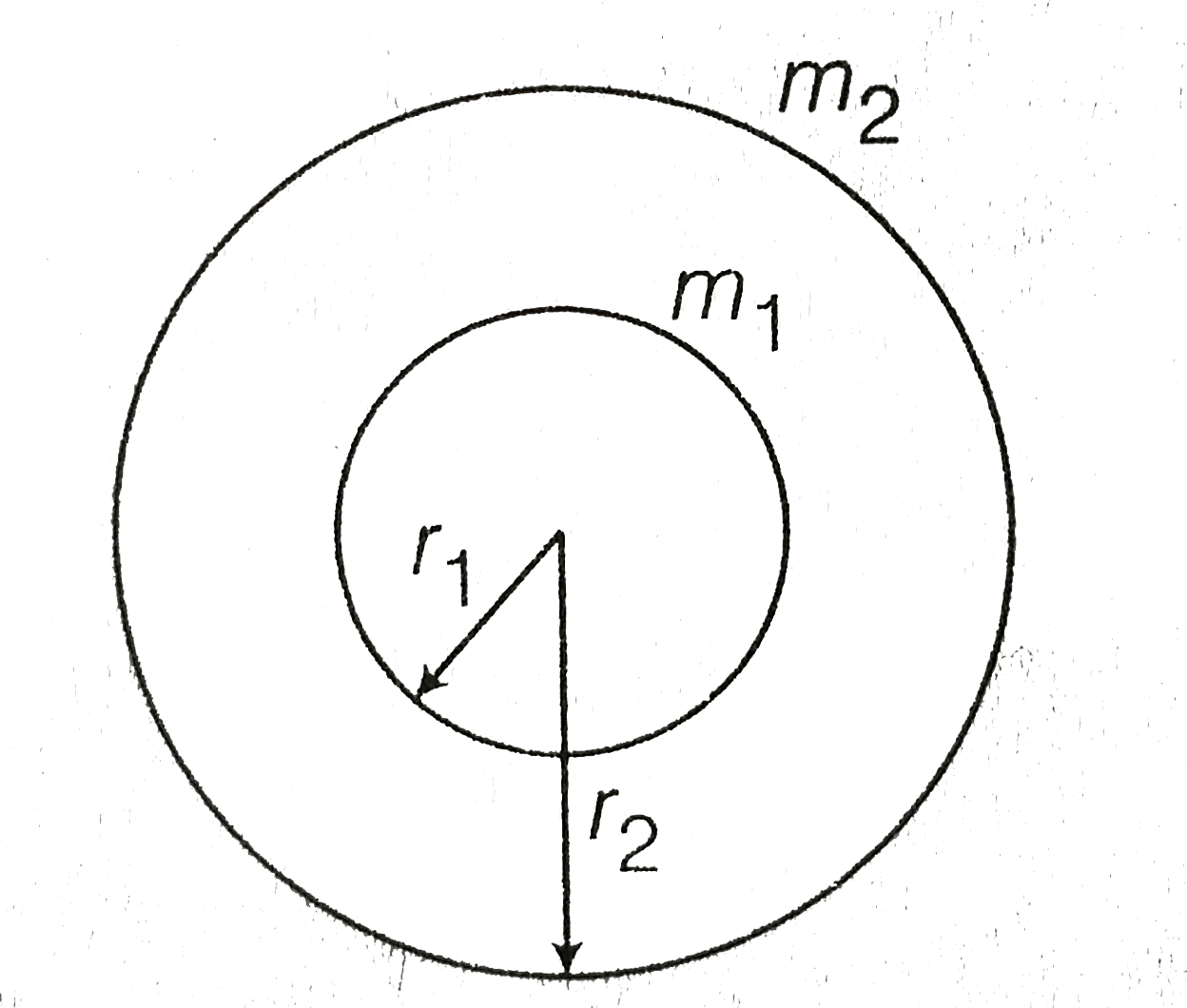
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionTwo particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
View SolutionThe magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionTwo particles of mass M and 2M are at a distance D apart. Under their mutual force of attraction they start moving towards each other. The acceleration of their centre of mass when they are D/2 apart is :
View Solution
