Two particles A1andB2 of masses m1andm2(m1>m2) have the same de Broglie wavelength . Then
their momenta are the same.
their energies are the same
the energy of A1 is less than the energy of A2
the energy of A1 is more than the energy of A2
The correct Answer is:A, C
To solve the problem, we need to analyze the relationship between the masses of two particles and their de Broglie wavelengths. Let's break it down step by step:
Step 1: Understanding de Broglie Wavelength
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
Step 2: Momentum of the Particles
The momentum (p) of a particle can also be expressed in terms of its mass (m) and velocity (v):
p=mv
Thus, for two particles A1 and B2 with masses m1 and m2 (where m1>m2), we can write:
λ1=hm1v1andλ2=hm2v2
Step 3: Setting the Wavelengths Equal
Since both particles have the same de Broglie wavelength, we can set the equations equal to each other:
hm1v1=hm2v2
By canceling h from both sides, we get:
1m1v1=1m2v2
Cross-multiplying gives us:
m2v2=m1v1
Step 4: Analyzing the Relationship
From the equation m2v2=m1v1, we can express the velocities in terms of each other:
v2=m1m2v1
Since m1>m2, it follows that v2>v1. This implies that the particle with the smaller mass (particle B2) must have a greater velocity to maintain the same de Broglie wavelength.
Step 5: Kinetic Energy Comparison
The kinetic energy (K) of a particle is given by:
K=12mv2
Substituting for v from our earlier relationship:
K1=12m1v21andK2=12m2v22
Substituting v2=m1m2v1 into the kinetic energy of particle B2:
K2=12m2(m1m2v1)2=12m2m21m22v21=12m21m2v21
Now, comparing K1 and K2:
K1=12m1v21andK2=12m21m2v21
Since m1>m2, it follows that K2>K1.
Conclusion
Thus, we conclude that:
- The momenta of both particles are equal.
- The kinetic energy of particle B2 is greater than that of particle A1.
Final Answer
The correct conclusion is that the kinetic energy of B2 is greater than that of A1.
---
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
The momentum (p) of a particle can also be expressed in terms of its mass (m) and velocity (v):
p=mv
Thus, for two particles A1 and B2 with masses m1 and m2 (where m1>m2), we can write:
λ1=hm1v1andλ2=hm2v2
Since both particles have the same de Broglie wavelength, we can set the equations equal to each other:
hm1v1=hm2v2
By canceling h from both sides, we get:
1m1v1=1m2v2
Cross-multiplying gives us:
m2v2=m1v1
From the equation m2v2=m1v1, we can express the velocities in terms of each other:
v2=m1m2v1
Since m1>m2, it follows that v2>v1. This implies that the particle with the smaller mass (particle B2) must have a greater velocity to maintain the same de Broglie wavelength.
The kinetic energy (K) of a particle is given by:
K=12mv2
Substituting for v from our earlier relationship:
K1=12m1v21andK2=12m2v22
Substituting v2=m1m2v1 into the kinetic energy of particle B2:
K2=12m2(m1m2v1)2=12m2m21m22v21=12m21m2v21
Now, comparing K1 and K2:
K1=12m1v21andK2=12m21m2v21
Since m1>m2, it follows that K2>K1.
Thus, we conclude that:
- The momenta of both particles are equal.
- The kinetic energy of particle B2 is greater than that of particle A1.
The correct conclusion is that the kinetic energy of B2 is greater than that of A1.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - NCERT FILE (NCERT - Exemplar Problems - Subjective Questions (Very Short Answer Type Questions))
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - NCERT FILE (NCERT - Exemplar Problems - Subjective Questions (Short Answer Type Questions))
6 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - NCERT FILE (NCERT - Exemplar Problems - Objective Questions (Multiple Choice Questions (Type - I)))
8 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
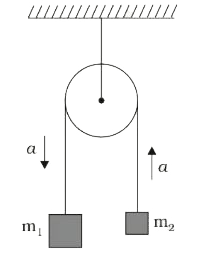
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
View SolutionA partical of mass M at rest decays into two Particles of masses
m1andm2 having non-zero velocities. The ratio of the de - Broglie wavelengths
of the particles λ1∣λ2 is
(a) m1/m2 (b)m2/m1 (c ) 1 (d)√,2/√_1
View Solution
Knowledge Check
Two particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
Atheir momenta are the sameBtheir energies are the sameCenergy of A1 is less than the energy of A2Denergy of A1, is more than the energy of A2A praticle of mass M at rest decays into two particle of masses m1 and m2, having non-zero velocities. The ratio of the de Broglie wavelength of the particles λ1λ2 is
Am1m2Bm2m1C1D√m2√m1A particle of mass M at rest decay's into two particle of masses m1 and m2 having non zero velocity. The ratio of the de Broglie wavelengths of the masses λ1/λ2 is
Am1/m2Bm2/m1C1.0D√m1/√m2
A particle of mass 3m at rest decays into two particles of masses m and 2m having non-zero velocities. The ratio of the de Broglie wavelengths of the particles (λ1λ2) is
View SolutionTwo particles of masses m and 2m have equal kinetic energies. Their de Broglie wavelengths area in the ratio of:
View SolutionTwo particles of masses m and 2m have equal kinetic energies. Their de Broglie wavelengths area in the ratio of:
View SolutionA particle of mass 4m at rest decays into two particles of masses m and 3m having non-zero velocities. The ratio of the de-Broglie wavelengths of the particles 1 and 2 is
View SolutionA particle of mass 4m at rest decays into two particles of masses m and 3m having nonzero velocities. The ratio of the de Broglie wavelengths of the particles 1 and 2 is (take h = 6.6×10−34m2kgs−1 )
View Solution
