A partical of mass M at rest decays into two Particles of masses
m1andm2 having non-zero velocities. The ratio of the de - Broglie wavelengths
of the particles λ1∣λ2 is
(a) m1/m2 (b)m2/m1 (c ) 1 (d)√,2/√_1
The correct Answer is:A, C
From the law of conservation of momentum,
P1=P2 (in opposite directions)
Now, de-Broglie wavelength is given by
λ=hPwhereh=Planckconstant<br>Sincemagnitdueofmomentum(p)of⊥hthepartic≤sisequal,∴lambda_1 = lambda_2<br>orlambda_1//lambda_2 = 1
Therefore, the correct option is (c ).
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Example Type 1
2 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 1EXERCISE - Example Type 2
6 Videos
- MODERN PHYSICSBOOK - DC PANDEYCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEYCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
A particle of a mass M at rest decays into two particles of masses m1andm2 having non-zero velocities. What is the ratio of the de-Broglie wavelength of the two particles?
View SolutionA particle of mass M at rest decays into two particles of masses m1andm2 having velocities V1andV2 respectively. Find the ratio of de- Broglie wavelengths of the two particles
View Solution
Knowledge Check
A praticle of mass M at rest decays into two particle of masses m1 and m2, having non-zero velocities. The ratio of the de Broglie wavelength of the particles λ1λ2 is
Am1m2Bm2m1C1D√m2√m1A particle of mass 4m at rest decays into two particles of masses m and 3m having non-zero velocities. The ratio of the de-Broglie wavelengths of the particles 1 and 2 is
A12B14C2D1A particle of mass 3m at rest decays into two particles of masses m and 2m having non-zero velocities. The ratio of the de Broglie wavelengths of the particles (λ1λ2) is
A12B14C2Dnone of these
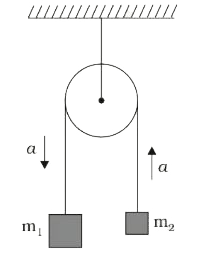
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
View SolutionA particle of mass M at rest decay's into two particle of masses m1 and m2 having non zero velocity. The ratio of the de Broglie wavelengths of the masses λ1/λ2 is
View SolutionA particle of mass 5M at rest decays into two particle of masses 2 m and 3 m having non zero velocities. The ratio of de - broglie wavelengh of the particles is
View SolutionA particle of mass 3 m at rest decay Into two particles of masses m and 2m having non-zero velocities. What is the ratio of the de-Broglie wavelengths of the particle (λ1/λ2).
View SolutionA particle of mass 4m at rest decays into two particles of masses m and 3m having nonzero velocities. The ratio of the de Broglie wavelengths of the particles 1 and 2 is (take h = 6.6×10−34m2kgs−1 )
View Solution
