The hydrogen atom in its ground state is excited by means of monochromatic radiation. Its resulting spectrum has six different lines. These radiations are incident on a metal plate. It is observed that only two of them are responsible for photoelectric effect. if the ratio of maximum kinetic energy of photoelectrons is the two cases is 5 then find the work function of the metal.
The correct Answer is:A, B
K1K2=5
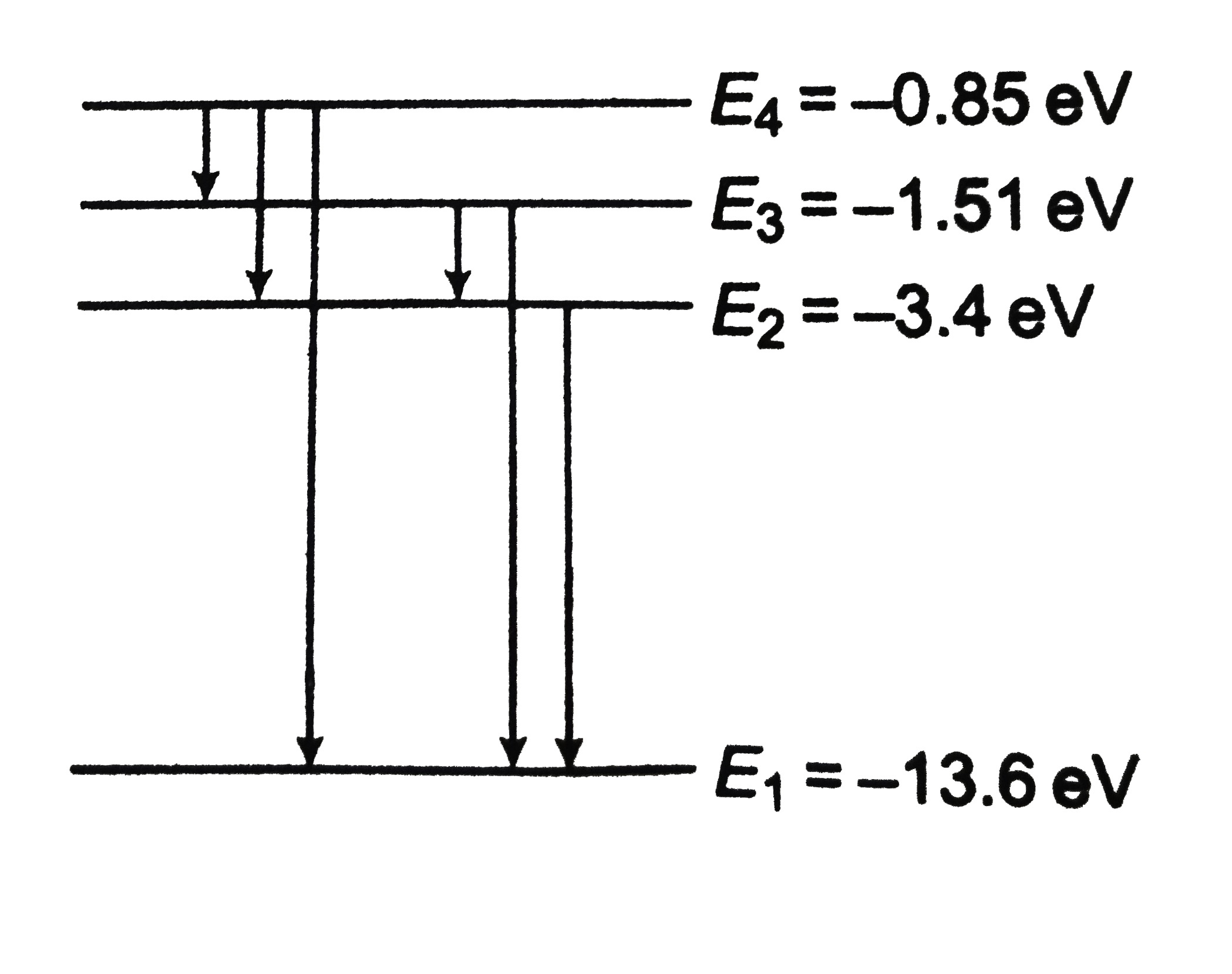
ΔE1−W)ΔE2−W=5…(i)
Here, ΔE1=E4−E1=12.75eV
and ΔE2=E3−E1=12.09eV
Substituting in Eq. (i) and solving, we get
W = 11.925 eV.
Related Playlists
Similar Questions
The hydrogen atom in the ground state is excited by means of monochromatic radiation of wavelength xA0 The resulting spectrum consists of 15 different lines. Calculate the value of x.
View SolutionA hydrogen atom in the ground state is excited by monochromatic radiation of wavelength λA. The resulting spectrum consits of maximum 15 different lines. What is the wavelength λ?
View SolutionHydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength 975A∘. How many different lines are possible in the resulting spectrum? Calculate the longest wavelength amongst them.
View SolutionHydrogen atom in ground state is excited by a monochromatic radiation of λ=975Å. Number of spectral lines in the resulting spectrum emitted will be
View SolutionHydrogen atom is ground state is excied by mean of monochromatic radiation of wavelength 975Å How many asume different lines are possible is the resulting spactrum ? Calculate the lorgest energy for hydrogen atom as 13.6eV
View SolutionThe hydrogen atom in the ground state is excited by mass of monchromatic radiations of wavelength
λÅ . The resulting spectrum consists fo maximum 15 different lines . What is the value of λ ? (RH=109737cm−1).View SolutionA gas of hydrogen atoms in its ground state, is excited by means of monochromatic radiation of wavelength 975A0. How many different spectral lines are possible in the resulting spectrum? (hc=12431.25eV−A0)
View SolutionHydrogen atom is its ground state is excited by means of monochromatic radiation of wavelength 1023Å. How many different lines are possible in the resulting spectrum? Calculate the longes wavelength among them. You may assume the ionization energy of hydrogen atom as 13.6 eV.
View SolutionH atom in its ground state is excited by means of a radiation of λ=970.6 Å. How many different wavelengths are possible in the resulting emission spectrum ?
View SolutionHydrogen atom in this ground state is excited by means of monochromatic radiation of wavelength 975Å. How many different lines are possible in the resulting spectrum? Calculate the longest wavelength amongst them. You may assume the ionization energy for hydrogen atom is 13.6eV
View Solution


