Two bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
To solve the problem, we need to find the position where the gravitational field due to two masses m1 and m2 is zero, and then calculate the gravitational potential at that position.
1. Understanding the Setup:
- We have two masses m1 and m2 separated by a distance d.
- Let’s denote the position where the gravitational field is zero as point P, which is at a distance x from mass m1 and d−x from mass m2.
2. Setting Up the Gravitational Fields:
- The gravitational field E1 due to mass m1 at point P is given by:
E1=Gm1x2
- The gravitational field E2 due to mass m2 at point P is given by:
E2=Gm2(d−x)2
3. Condition for Zero Gravitational Field:
- For the net gravitational field at point P to be zero, we set E1 equal to E2:
Gm1x2=Gm2(d−x)2
- We can cancel G from both sides:
m1x2=m2(d−x)2
4. Cross-Multiplying:
- Cross-multiplying gives:
m1(d−x)2=m2x2
5. Expanding the Equation:
- Expanding the left side:
m1(d2−2dx+x2)=m2x2
- Rearranging gives:
m1d2−2m1dx+m1x2−m2x2=0
- This simplifies to:
m1d2−2m1dx+(m1−m2)x2=0
6. Using the Quadratic Formula:
- This is a quadratic equation in x. We can use the quadratic formula x=−b±√b2−4ac2a where:
- a=m1−m2
- b=−2m1d
- c=m1d2
- The solution for x will be:
x=2m1d±√(2m1d)2−4(m1−m2)(m1d2)2(m1−m2)
7. Finding the Gravitational Potential:
- The gravitational potential V at point P is given by:
V=−Gm1x−Gm2d−x
- Substituting the value of x from our earlier calculation into this equation will yield the potential.
8. Final Expression for Potential:
- After substituting and simplifying, we arrive at:
V=−Gd(m1+m2+2√m1m2)
Conclusion:
Thus, we have shown that the gravitational potential at the point where the gravitational field due to the two masses is zero is given by:
V=−Gd(m1+m2+2√m1m2)
- We have two masses m1 and m2 separated by a distance d.
- Let’s denote the position where the gravitational field is zero as point P, which is at a distance x from mass m1 and d−x from mass m2.
- The gravitational field E1 due to mass m1 at point P is given by:
E1=Gm1x2
- The gravitational field E2 due to mass m2 at point P is given by:
E2=Gm2(d−x)2
- For the net gravitational field at point P to be zero, we set E1 equal to E2:
Gm1x2=Gm2(d−x)2
- We can cancel G from both sides:
m1x2=m2(d−x)2
- Cross-multiplying gives:
m1(d−x)2=m2x2
- Expanding the left side:
m1(d2−2dx+x2)=m2x2
- Rearranging gives:
m1d2−2m1dx+m1x2−m2x2=0
- This simplifies to:
m1d2−2m1dx+(m1−m2)x2=0
- This is a quadratic equation in x. We can use the quadratic formula x=−b±√b2−4ac2a where:
- a=m1−m2
- b=−2m1d
- c=m1d2
- The solution for x will be:
x=2m1d±√(2m1d)2−4(m1−m2)(m1d2)2(m1−m2)
- The gravitational potential V at point P is given by:
V=−Gm1x−Gm2d−x
- Substituting the value of x from our earlier calculation into this equation will yield the potential.
- After substituting and simplifying, we arrive at:
V=−Gd(m1+m2+2√m1m2)
Thus, we have shown that the gravitational potential at the point where the gravitational field due to the two masses is zero is given by:
V=−Gd(m1+m2+2√m1m2)
Topper's Solved these Questions
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - SELECTED PROBLEMS[FROM GRAVITATIONAL POTENTIAL ENERGY]
4 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - SELECTED PROBLEMS[FROM ESCAPE VELOCITY ]
20 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - SELECTED PROBLEMS[FROM VARIATION OF G WITH ALTITUDE, LATITUDE, DEPTH]
14 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)
21 Videos
Similar Questions
Two bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero,the gravitational potential will be :-
View Solution
Knowledge Check
Two stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
A2π√r32G(m1+m2)B2π√r3(m1+m2)2G(m1m2)C2π√2r3G(m1+m2)D2π√r3G(m1+m2)
Two bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point due to mass m on the line joining where gravitational field is zero
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo point masses having mass m and 2m are placed at distance d . The point on the line joining point masses , where gravitational field intensity is zero will be at distance
View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

View SolutionTwo bodies of mass 102 kg and 103 kg are lying 1 m apart .
The gravitational potential at the mid-point of the line joining them is
View SolutionTwo particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
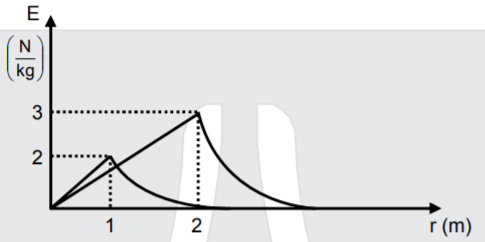
View SolutionTwo spherical bodies of mass m1 & m2 are having radius 1 m & 2 m respectively. The gravitational field of the two bodies with their radial distance is shown below. The value of m1m2 is
 -
-
View Solution
