A student is asked to connected four cells of e.m.f of 1 V and internal resistance 0.5 ohm in series with a external resistance of 1 ohm. But one cell is wrongly connected by him with its terminal reversed, the current in the circuit is
13A
23A
34A
43A
The correct Answer is:B
To solve the problem, we need to analyze the circuit step by step.
Step 1: Determine the Net EMF of the Circuit
In the circuit, we have four cells, each with an EMF of 1 V. However, one cell is connected in reverse. Therefore, the net EMF (E_net) can be calculated as follows:
- Three cells contribute positively: 1+1+1=3V
- One cell contributes negatively due to the reverse connection: −1V
Thus, the total EMF is:
Enet=3V−1V=2V
Step 2: Calculate the Total Internal Resistance
Each cell has an internal resistance of 0.5Ω. Since there are four cells in series, the total internal resistance (R_internal) is:
Rinternal=4×0.5Ω=2Ω
Step 3: Determine the Total Resistance in the Circuit
The total resistance in the circuit (R_total) includes the external resistance (1 Ω) and the total internal resistance (2 Ω):
Rtotal=Rexternal+Rinternal=1Ω+2Ω=3Ω
Step 4: Calculate the Current in the Circuit
Using Ohm's law, the current (I) in the circuit can be calculated using the formula:
I=EnetRtotal
Substituting the values we found:
I=2V3Ω=23A
Final Answer
The current in the circuit is:
I=23A
---
In the circuit, we have four cells, each with an EMF of 1 V. However, one cell is connected in reverse. Therefore, the net EMF (E_net) can be calculated as follows:
- One cell contributes negatively due to the reverse connection: −1V
Enet=3V−1V=2V
Each cell has an internal resistance of 0.5Ω. Since there are four cells in series, the total internal resistance (R_internal) is:
Rinternal=4×0.5Ω=2Ω
The total resistance in the circuit (R_total) includes the external resistance (1 Ω) and the total internal resistance (2 Ω):
Rtotal=Rexternal+Rinternal=1Ω+2Ω=3Ω
Using Ohm's law, the current (I) in the circuit can be calculated using the formula:
I=EnetRtotal
Substituting the values we found:
I=2V3Ω=23A
The current in the circuit is:
I=23A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (Linked Comprehension Type Questions))
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - II LEVEL-II (ADVANCED) (Integer Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Four cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View Solution24 cells of emf 1.5V each having internal resistance of 1 ohm are connected to an external resistance of 1.5 ohms. To get maximum current,
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionTen cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View Solutionn identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
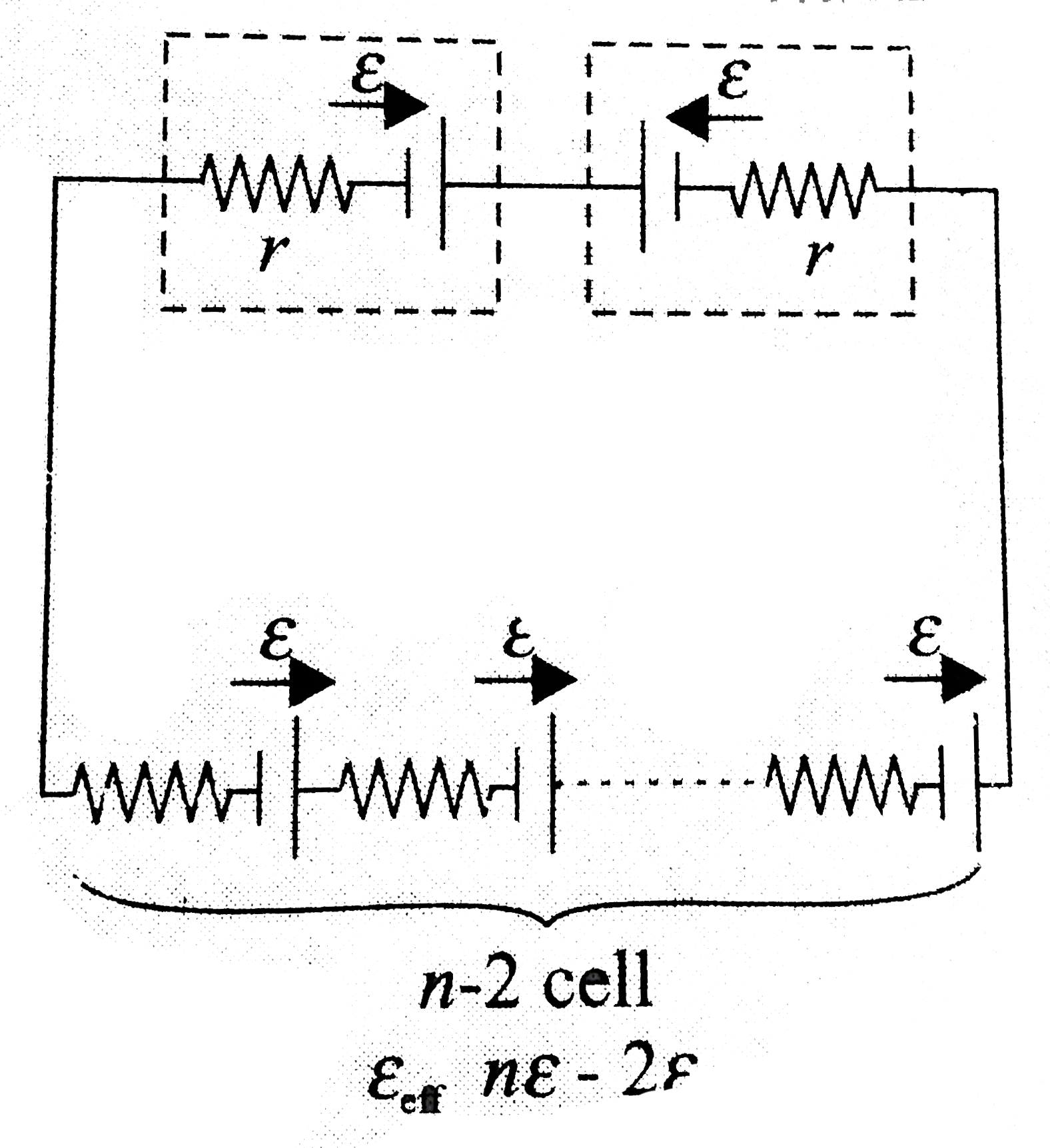
View Solution
