Two small balls having equal positive charge Q C on each are suspended by two insulating strings of equal length L metre, from a hook fixed to a stand. The whole setup is taken into space where there is no gravity (state of weightlessness). Then the angle θ between the two strings is
0∘
90∘
180∘
0∘<θ<180∘
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the two charged balls when they are suspended in a weightless environment.
1. Understanding the Setup:
- We have two small balls, each with a positive charge Q, suspended by insulating strings of equal length L.
- In a weightless environment, the gravitational force acting on the balls is negligible.
2. Forces Acting on the Balls:
- In the absence of gravity, the only force acting on each ball is the electrostatic repulsion between the two positively charged balls.
- According to Coulomb's law, the force F between the two charges is given by:
F=k⋅Q2r2
where k is Coulomb's constant and r is the distance between the two charges.
3. Geometry of the Setup:
- Let the angle between the two strings be θ.
- The distance r between the two balls can be expressed in terms of L and θ:
r=2Lsin(θ2)
4. Equilibrium Condition:
- In the weightless condition, the electrostatic force F must balance the tension in the strings.
- The tension T in each string can be resolved into two components: one that acts vertically (which is zero in this case) and one that acts horizontally (which provides the necessary centripetal force).
- Since there is no vertical force, we can focus on the horizontal component:
Tsin(θ2)=F
5. Substituting for F:
- From Coulomb's law:
Tsin(θ2)=k⋅Q2(2Lsin(θ2))2
6. Solving for θ:
- Since the tension T is not acting vertically, we can simplify the equation:
Tsin(θ2)=k⋅Q24L2sin2(θ2)
- Rearranging gives:
T=k⋅Q24L2sin(θ2)
- In the absence of gravity, the strings will align themselves to minimize potential energy, leading to a configuration where the angle θ approaches 180∘.
7. Conclusion:
- Therefore, the angle θ between the two strings in a weightless environment is:
θ=180∘
Final Answer:
The angle θ between the two strings is 180∘.
- We have two small balls, each with a positive charge Q, suspended by insulating strings of equal length L.
- In a weightless environment, the gravitational force acting on the balls is negligible.
- In the absence of gravity, the only force acting on each ball is the electrostatic repulsion between the two positively charged balls.
- According to Coulomb's law, the force F between the two charges is given by:
F=k⋅Q2r2
where k is Coulomb's constant and r is the distance between the two charges.
- Let the angle between the two strings be θ.
- The distance r between the two balls can be expressed in terms of L and θ:
r=2Lsin(θ2)
- In the weightless condition, the electrostatic force F must balance the tension in the strings.
- The tension T in each string can be resolved into two components: one that acts vertically (which is zero in this case) and one that acts horizontally (which provides the necessary centripetal force).
- Since there is no vertical force, we can focus on the horizontal component:
Tsin(θ2)=F
- From Coulomb's law:
Tsin(θ2)=k⋅Q2(2Lsin(θ2))2
- Since the tension T is not acting vertically, we can simplify the equation:
Tsin(θ2)=k⋅Q24L2sin2(θ2)
- Rearranging gives:
T=k⋅Q24L2sin(θ2)
- In the absence of gravity, the strings will align themselves to minimize potential energy, leading to a configuration where the angle θ approaches 180∘.
- Therefore, the angle θ between the two strings in a weightless environment is:
θ=180∘
The angle θ between the two strings is 180∘.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I80videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX42videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
Similar Questions
Two small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
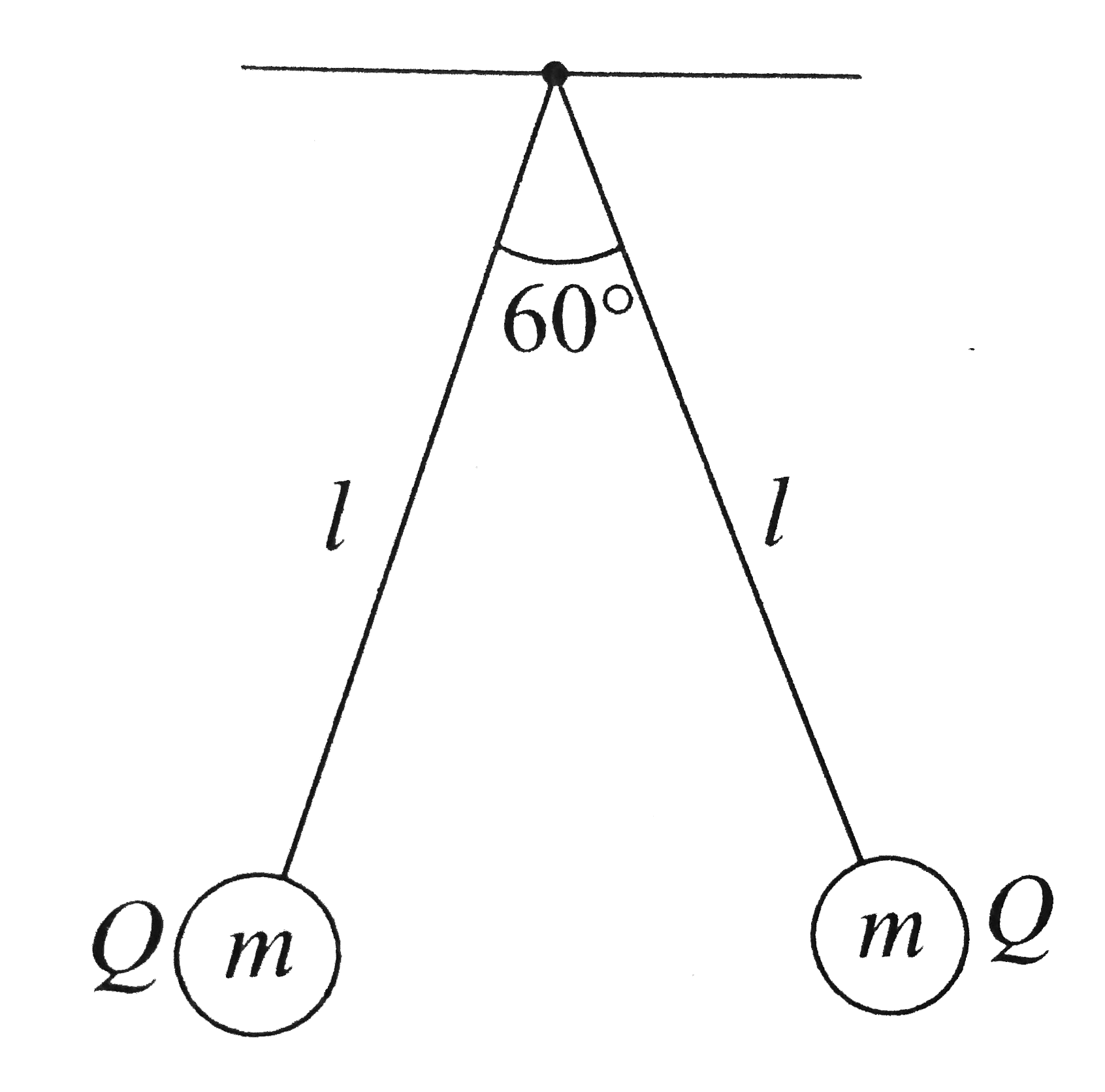 View Solution
View SolutionTwo similar balls having equal positive charge q are suspanded by two insulating stings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two ?
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small spherical balls each carrying a charge Q=10μC are suspended by two insulating threads of equal lengths 1cm each, from a point fixed in the ceiling. It is found that in equilibrium threads are sepreated by an angle 60∘ between them, as shown in figure. What is the tension in the threads
(Given 14πε0=9×109Nm/C2 )
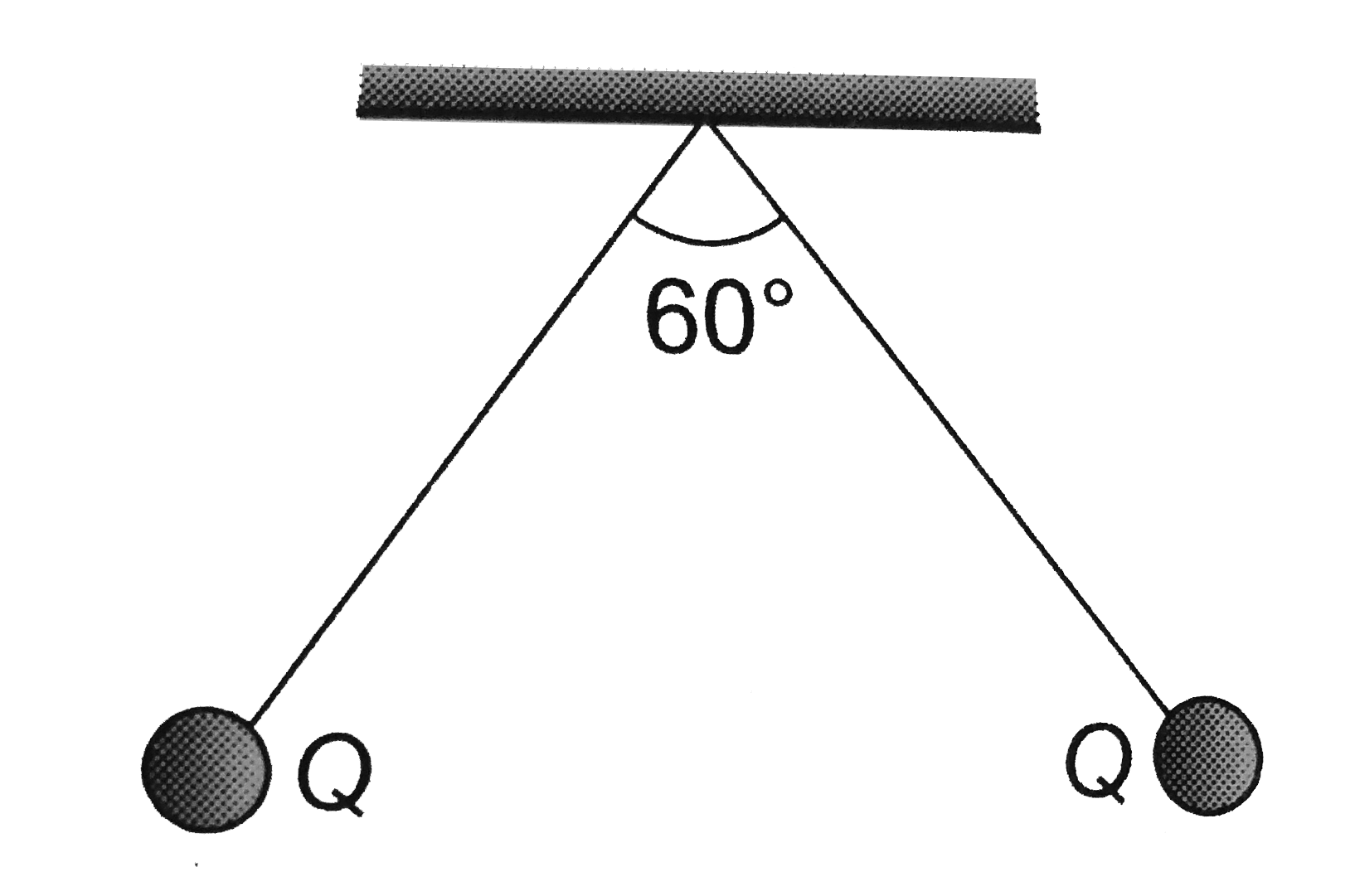 View Solution
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
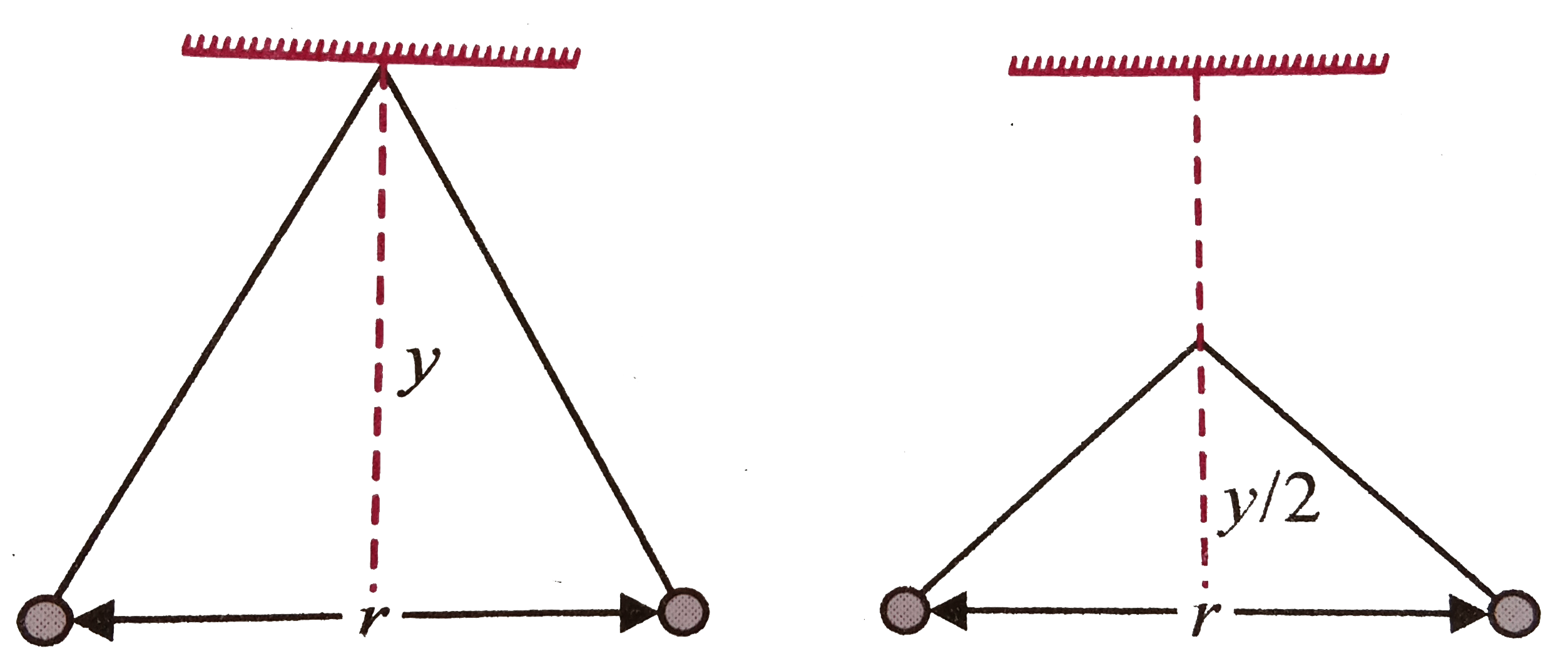 View Solution
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo charged particles having charge 2.0×10−8C. Each are joined by an isolating string of length 1m and the system is kept on a smooth horizontal task. The tension in the string.
View Solution
