Two charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
To find the tension in the string connecting the two charged particles, we can follow these steps:
Step 1: Identify the relevant formula
The tension in the string is equal to the electrostatic force between the two charged particles. The formula for the electrostatic force F between two point charges is given by Coulomb's law:
F=kQ1Q2R2
where:
- k is Coulomb's constant, approximately 9×109N m2/C2,
- Q1 and Q2 are the magnitudes of the charges,
- R is the distance between the charges.
Step 2: Substitute the values into the formula
In this case, both charges Q1 and Q2 are 2.0×10−8C and the distance R is 1m. Therefore, we can substitute these values into the formula:
F=9×109(2.0×10−8)(2.0×10−8)(1)2
Step 3: Calculate the force
Now we can calculate the force:
F=9×109(4.0×10−16)1
F=9×109×4.0×10−16
F=36×10−7N
F=3.6×10−6N
Step 4: Conclusion
Thus, the tension in the string is:
Tension=3.6×10−6N
The tension in the string is equal to the electrostatic force between the two charged particles. The formula for the electrostatic force F between two point charges is given by Coulomb's law:
F=kQ1Q2R2
where:
- k is Coulomb's constant, approximately 9×109N m2/C2,
- Q1 and Q2 are the magnitudes of the charges,
- R is the distance between the charges.
In this case, both charges Q1 and Q2 are 2.0×10−8C and the distance R is 1m. Therefore, we can substitute these values into the formula:
F=9×109(2.0×10−8)(2.0×10−8)(1)2
Now we can calculate the force:
F=9×109(4.0×10−16)1
F=9×109×4.0×10−16
F=36×10−7N
F=3.6×10−6N
Thus, the tension in the string is:
Tension=3.6×10−6N
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:question for short answer
Explore 14 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 1
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:worked out Examples
Explore 19 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT THROUGH GASESExercise:Short answer
Explore 6 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Questions for short answer
Explore 9 Videos
Similar Questions
Two charged particles having charge 2.0×10−8C. Each are joined by an isolating string of length 1m and the system is kept on a smooth horizontal task. The tension in the string.
View Solution(i) Two charged particles having vharge 4.0×10−6C and mass 24×10−3Kg each are joining by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
(ii) If suddenly string is cut then what is the acceleration of each particle ?
(iii) Are they having equal acceleration ?
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q=1μC , mass of each particle m=6g. The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface.

What is the tension in the string?
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionTwo charged particles, having equal charges of 2.0×10−5C each, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process.
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the position shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
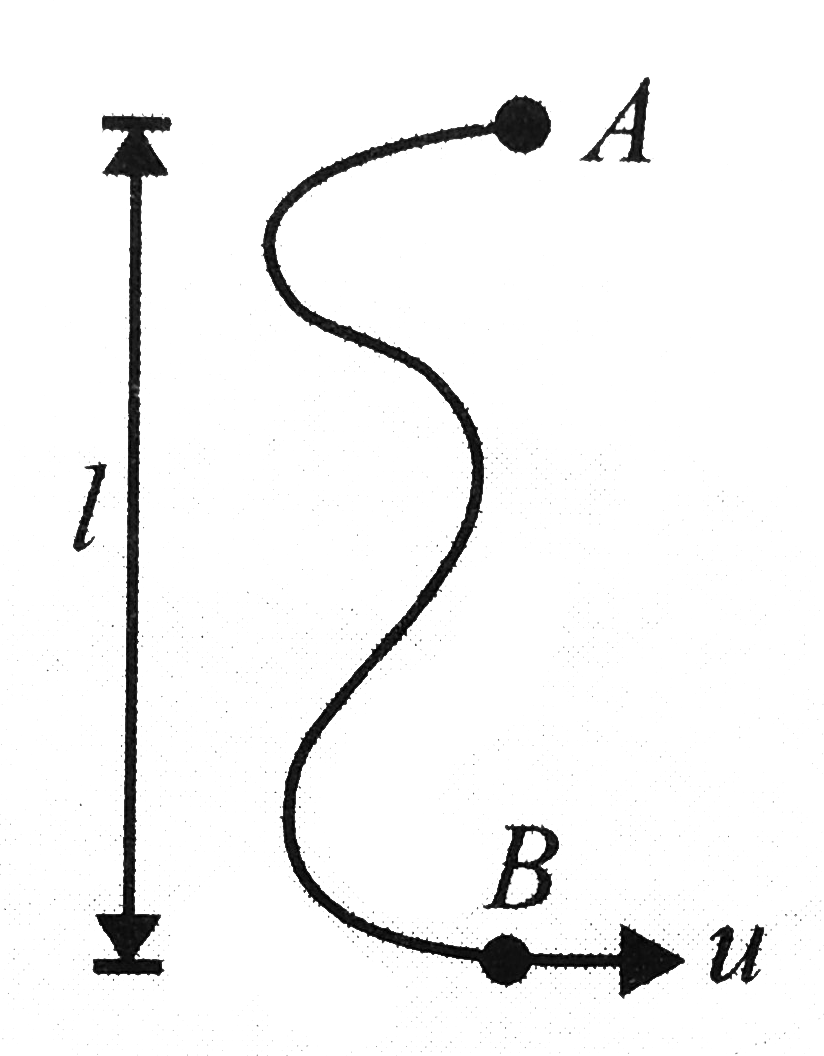
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
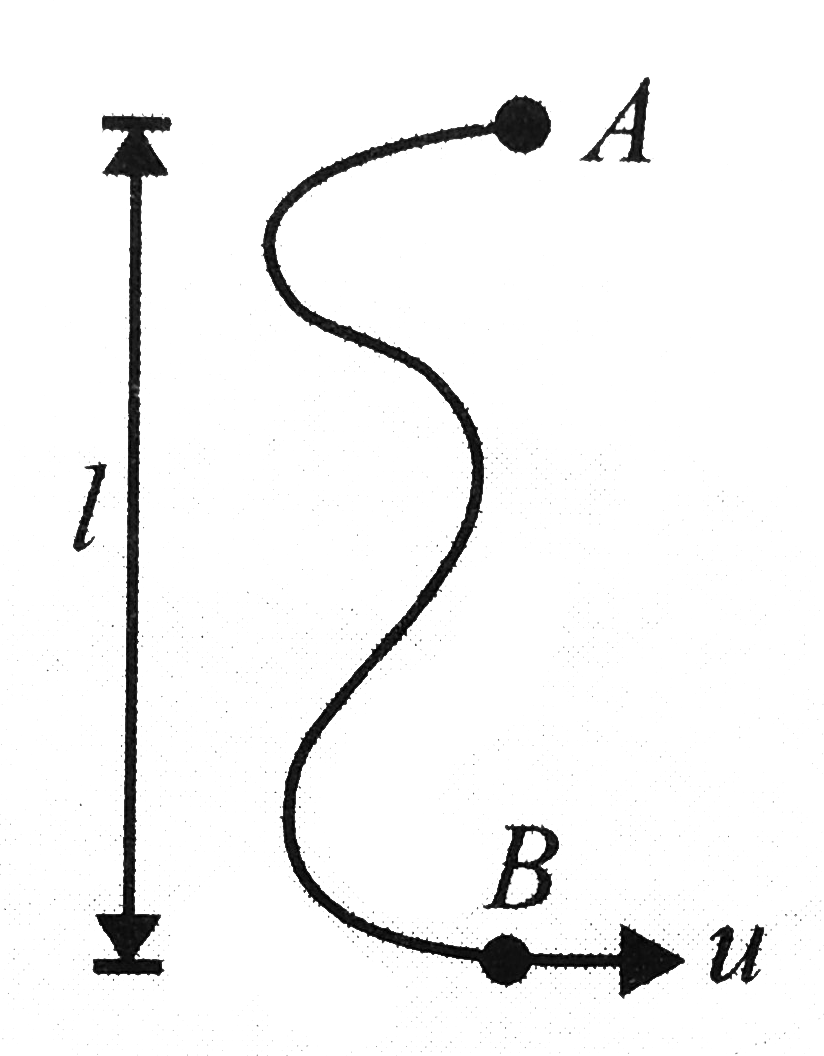
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionTwo particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is

View Solution

