Two identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. in equilibrium, the separation between the balls in 3 cm. Find the mass of each ball and the tension in the strings. the charge on each ball of a magnitude 2.0×10−8C.
To solve the problem step by step, we will follow these steps:
Step 1: Understand the setup
Two identical pith balls are charged and suspended from a horizontal rod. The length of the strings is 20 cm, the distance between the suspension points is 5 cm, and the distance between the balls in equilibrium is 3 cm. The charge on each ball is Q=2.0×10−8C.
Step 2: Calculate the electrostatic force between the balls
Using Coulomb's law, the electrostatic force F between the two charged balls is given by:
F=kQ2r2
Where:
- k=9×109Nm2/C2 (Coulomb's constant)
- Q=2.0×10−8C
- r=0.03m (the distance between the balls in meters)
Substituting the values:
F=9×109(2.0×10−8)2(0.03)2
Calculating F:
F=9×1094.0×10−160.0009=9×109×4.444×10−13=4.0×10−3N
Step 3: Analyze the forces acting on the balls
In equilibrium, the forces acting on each ball are:
- The tension T in the string
- The weight mg acting downwards
- The electrostatic force F acting horizontally
Step 4: Resolve the forces
Let θ be the angle the string makes with the vertical. We can express sinθ and cosθ in terms of the geometry of the system.
From the geometry:
- The vertical distance from the suspension point to the ball is Lcosθ
- The horizontal distance from the suspension point to the ball is Lsinθ
Using the small angle approximation, we can say:
sinθ≈3cm20cm=320=0.15
Step 5: Calculate the mass of each ball
Using the vertical force balance:
Tcosθ=mg
And the horizontal force balance:
Tsinθ=F
From the second equation, we can express T:
T=Fsinθ
Substituting F and sinθ:
T=4.0×10−30.15=2.67×10−2N
Now substituting T back into the first equation to find m:
2.67×10−2cosθ=mg
Using cosθ≈√1−sin2θ≈√1−(0.15)2≈√0.9775≈0.99:
2.67×10−2×0.99=mg
Calculating mg:
mg≈2.64×10−2N
Using g=10m/s2:
m=2.64×10−210=2.64×10−3kg=2.64g
Step 6: Final results
- Mass of each ball: m≈2.64g
- Tension in the strings: T≈2.67×10−2N
Two identical pith balls are charged and suspended from a horizontal rod. The length of the strings is 20 cm, the distance between the suspension points is 5 cm, and the distance between the balls in equilibrium is 3 cm. The charge on each ball is Q=2.0×10−8C.
Using Coulomb's law, the electrostatic force F between the two charged balls is given by:
- k=9×109Nm2/C2 (Coulomb's constant)
- Q=2.0×10−8C
- r=0.03m (the distance between the balls in meters)
In equilibrium, the forces acting on each ball are:
- The tension T in the string
- The weight mg acting downwards
- The electrostatic force F acting horizontally
Let θ be the angle the string makes with the vertical. We can express sinθ and cosθ in terms of the geometry of the system.
- The vertical distance from the suspension point to the ball is Lcosθ
- The horizontal distance from the suspension point to the ball is Lsinθ
Using the vertical force balance:
- Mass of each ball: m≈2.64g
- Tension in the strings: T≈2.67×10−2N
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Two identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. in equilibrium, the separation between the balls in 3 cm. Find the mass of each ball and the tension in the strings. the charge on each ball of a magnitude 2.0×10−8C.
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
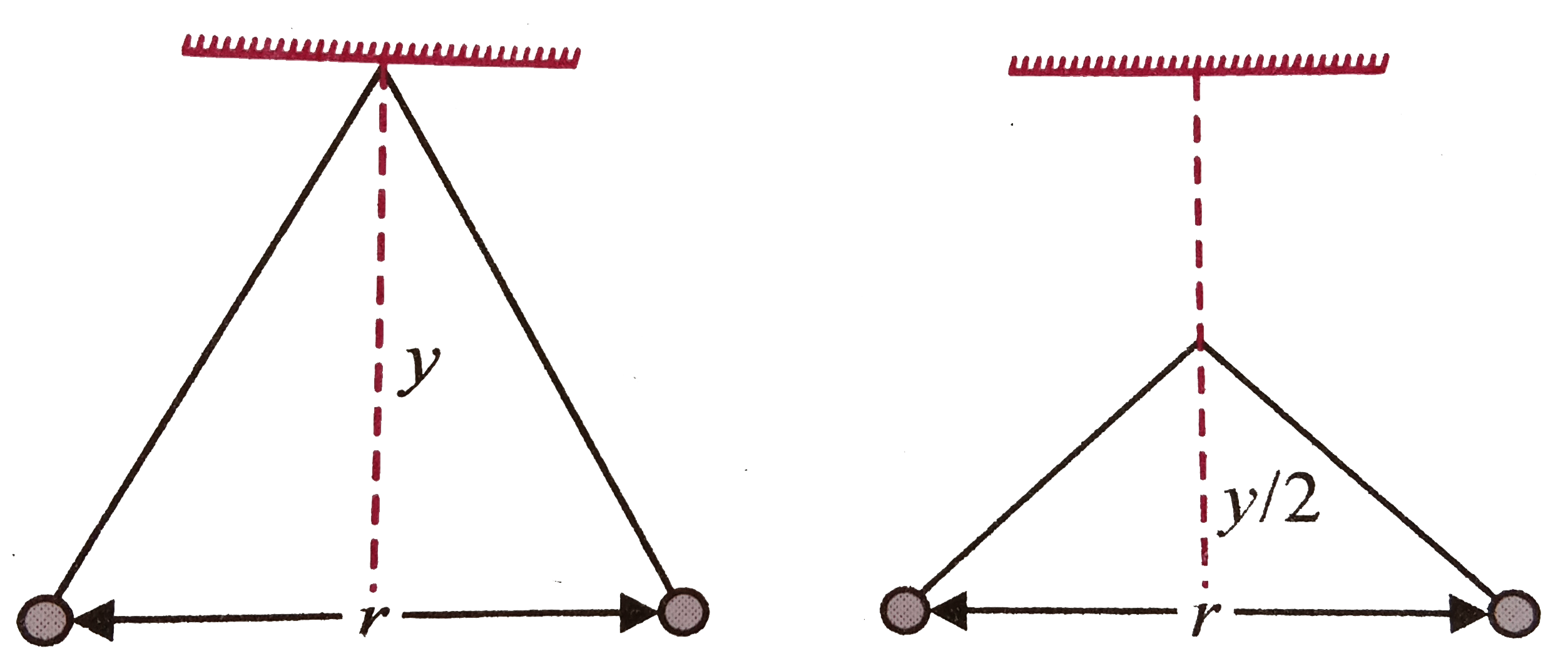
View SolutionTwo pitch balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become

View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionAssertion : Two identical balls are charged by q. They are suspended from a common point by two insulating threads l each. In equilibrium, the angle between the tension in the threads is 180∘. (Ignore gravity).
Reason : In equilibrium tension in the spring is
T=14πε0q.ql2
View SolutionTwo identical balls , each having a charge q and mass m , are suspended from a common point by two insultating strings each of length L. The balls are held at a separation x and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
View SolutionA body of mass 50 kg, suspended by two strings of lengths 30 cm and 40 cm fastend to two points in the same horizontal line 50 cm apart, is in equilibrium. Find the tension (in Newtons) in each string.
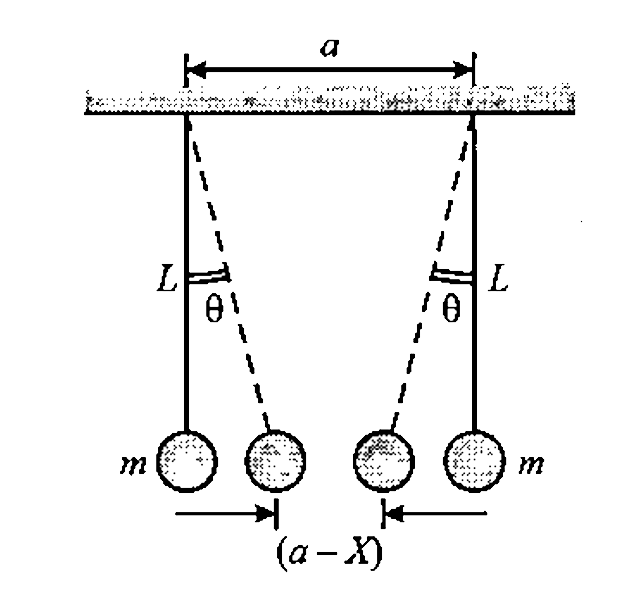
View SolutionTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
View Solution
