(A) : It is harder to open and shut the door if we apply force near the hinge.
(R ) : Torque due to a given force is maximum at hinge of the door.
Both (A) and (R ) are true and (R ) is the correct explanation of (A)
Both (A) and (R ) are true and (R ) is not the correct explanation of (A)
(A) is true but (R ) is false
Both (A) and (R ) are false
The correct Answer is:C
To solve the question, we need to analyze both the assertion (A) and the reason (R) provided.
Step 1: Understanding the Assertion
The assertion states that "It is harder to open and shut the door if we apply force near the hinge."
- When we apply a force near the hinge, the distance (r) from the hinge (the axis of rotation) to the point where the force is applied is small.
Step 2: Understanding Torque
Torque (τ) is defined as the product of the force (F) and the distance (r) from the axis of rotation to the point of force application:
τ=r×F
- If r is small, then the torque will also be small, which means the rotational effect of the force is reduced.
Step 3: Conclusion from the Assertion
Since the torque is less when the force is applied near the hinge, it becomes harder to open or shut the door. Therefore, the assertion (A) is true.
Step 4: Understanding the Reason
The reason states that "Torque due to a given force is maximum at the hinge of the door."
- This statement is incorrect. The torque is maximum when the force is applied at the farthest point from the hinge (the edge of the door) because this maximizes the distance (r).
Step 5: Conclusion from the Reason
Since the reason (R) is incorrect, we conclude that while the assertion (A) is true, the reason (R) is false.
Final Conclusion
- The assertion (A) is true.
- The reason (R) is false.
Thus, the correct answer is that the assertion is true and the reason is false.
---
The assertion states that "It is harder to open and shut the door if we apply force near the hinge."
- When we apply a force near the hinge, the distance (r) from the hinge (the axis of rotation) to the point where the force is applied is small.
Torque (τ) is defined as the product of the force (F) and the distance (r) from the axis of rotation to the point of force application:
τ=r×F
- If r is small, then the torque will also be small, which means the rotational effect of the force is reduced.
Since the torque is less when the force is applied near the hinge, it becomes harder to open or shut the door. Therefore, the assertion (A) is true.
The reason states that "Torque due to a given force is maximum at the hinge of the door."
- This statement is incorrect. The torque is maximum when the force is applied at the farthest point from the hinge (the edge of the door) because this maximizes the distance (r).
Since the reason (R) is incorrect, we conclude that while the assertion (A) is true, the reason (R) is false.
- The assertion (A) is true.
- The reason (R) is false.
Similar Questions
A : It is very difficult to open or close a door if force is applied near the hinge.
R : The moment of applied force is minimum near the hinge.
View SolutionWhy is it easier to open a door by applying the force at the free end of it.
View Solution(i) Write the expression for the magnetic moment (→m) due to a planar square loop of side 'l' carrying a steady current I in a vector form.
(ii) In figure., this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reasons to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

View SolutionA vertical rectangular door with its centre of gravity at O (see figure) is fixed on two hinges A and B along one vertical length side of the door. The entire weight of the door is supported by the hinge A. Then the free body force diagram for the door (the arrows indicate the direction of the forces) is

View SolutionThree particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View Solutionthe door of an almirah is 6 ft high, 1.5 ft wide and weights 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitude of the forces exerted by the hinges on the door are equal find this magnitude.
View Solutionthe door of an almirah is 6 ft high, 1.5 ft wide and weights 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitude of the forces exerted by the hinges on the door are equal find this magnitude.
View SolutionA rectangular loop of wire of size 4cm×10cm carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.

View SolutionA rectangular loop of wire of size 2cm×5cm carries a steady current of 1A. A straight long wire carrying 4 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the end
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
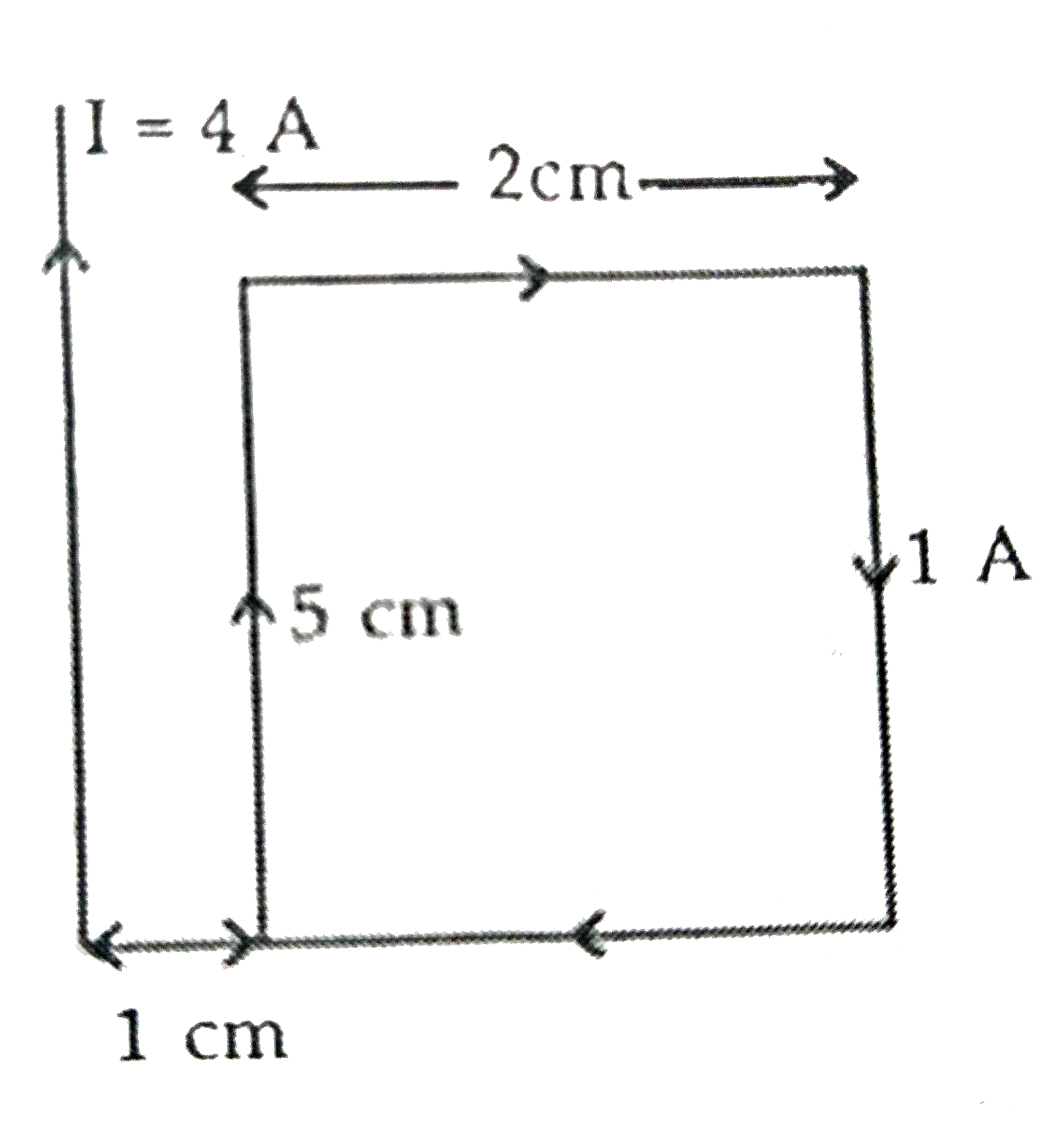
View SolutionA door 1.6 m wide requires a force of 1 N to be applied at the free end to open or close it. The force that is required at a point 0.4 m distant from the hinges for opening or closing the door is
View Solution
