the door of an almirah is 6 ft high, 1.5 ft wide and weights 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitude of the forces exerted by the hinges on the door are equal find this magnitude.
To solve the problem of finding the magnitude of the forces exerted by the hinges on the door of the almirah, we can follow these steps:
Step 1: Understand the Setup
The door is 6 ft high, 1.5 ft wide, and weighs 8 kg. The weight of the door acts downwards at its center of mass, which is at the midpoint of the door. The door is supported by two hinges located 1 ft from each end.
Step 2: Convert Weight to Newtons
The weight of the door in Newtons can be calculated using the formula:
Weight=mass×g
where g≈9.81m/s2 (acceleration due to gravity).
First, convert the mass from kg to Newtons:
Weight=8kg×9.81m/s2=78.48N
Step 3: Identify Forces at the Hinges
Let Ny be the vertical force exerted by each hinge and Nx be the horizontal force exerted by each hinge. Since the forces exerted by the two hinges are equal, we have:
Ny1=Ny2=Ny
Nx1=Nx2=Nx
Step 4: Apply Equilibrium Conditions
For the door to be in equilibrium, the sum of vertical forces and horizontal forces must be zero.
Vertical Forces:
Ny+Ny=Weight
2Ny=78.48
Ny=78.482=39.24N
Horizontal Forces:
Since the door is not moving horizontally, the horizontal forces must also balance:
Nx+Nx=0
This implies that Nx must be equal and opposite, but we will find Nx later.
Step 5: Calculate Torque
We will take moments about one of the hinges to find the torque. Let’s take moments about the hinge at the left side (1 ft from the left).
The weight acts at the center of the door, which is 0.75 ft from the left hinge (1.5 ft wide door). The distance from the left hinge to the center of mass is:
Distance=0.75ft−1ft=−0.25ft
This means the torque due to the weight is:
τ=Weight×Distance=78.48N×0.75ft
The torque due to the vertical forces at the right hinge (1.5 ft from the left hinge) is:
τ=Ny×1.5
Setting the clockwise torque equal to the counterclockwise torque:
78.48×0.75=Ny×1.5
Substituting Ny=39.24:
78.48×0.75=39.24×1.5
Step 6: Solve for Nx
From the equilibrium of torques, we can find Nx:
Since the net torque about the center of mass must also be zero, we can set up the equation:
Nx×2=Ny×1
Substituting Ny=39.24:
Nx×2=39.24
Nx=39.242=19.62N
Step 7: Resultant Force
The total force exerted by each hinge can be calculated using Pythagoras' theorem:
F=√N2x+N2y
F=√(19.62)2+(39.24)2
Calculating this gives:
F=√384.0644+1545.0576=√1929.122≈43.96N
Final Answer
The magnitude of the forces exerted by each hinge on the door is approximately 43.96N.
---
The door is 6 ft high, 1.5 ft wide, and weighs 8 kg. The weight of the door acts downwards at its center of mass, which is at the midpoint of the door. The door is supported by two hinges located 1 ft from each end.
The weight of the door in Newtons can be calculated using the formula:
Weight=mass×g
where g≈9.81m/s2 (acceleration due to gravity).
First, convert the mass from kg to Newtons:
Weight=8kg×9.81m/s2=78.48N
Let Ny be the vertical force exerted by each hinge and Nx be the horizontal force exerted by each hinge. Since the forces exerted by the two hinges are equal, we have:
Ny1=Ny2=Ny
Nx1=Nx2=Nx
For the door to be in equilibrium, the sum of vertical forces and horizontal forces must be zero.
Ny+Ny=Weight
2Ny=78.48
Ny=78.482=39.24N
Since the door is not moving horizontally, the horizontal forces must also balance:
Nx+Nx=0
This implies that Nx must be equal and opposite, but we will find Nx later.
We will take moments about one of the hinges to find the torque. Let’s take moments about the hinge at the left side (1 ft from the left).
Distance=0.75ft−1ft=−0.25ft
This means the torque due to the weight is:
τ=Weight×Distance=78.48N×0.75ft
τ=Ny×1.5
78.48×0.75=Ny×1.5
Substituting Ny=39.24:
78.48×0.75=39.24×1.5
From the equilibrium of torques, we can find Nx:
Since the net torque about the center of mass must also be zero, we can set up the equation:
Nx×2=Ny×1
Substituting Ny=39.24:
Nx×2=39.24
Nx=39.242=19.62N
The total force exerted by each hinge can be calculated using Pythagoras' theorem:
F=√N2x+N2y
F=√(19.62)2+(39.24)2
Calculating this gives:
F=√384.0644+1545.0576=√1929.122≈43.96N
The magnitude of the forces exerted by each hinge on the door is approximately 43.96N.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A rod of length 6m has a mass of 12kg. It is hined at one end of the rod at a distance of 3m below the water surface.
a.What must be the weight of a block that is attached to the other end of the rod so that 5m of the rod's length is under water?
b. Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of rod is 0.5.
 View Solution
View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is?
 View Solution
View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is
 View Solution
View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is
 View Solution
View SolutionFigure shows a convex lens of focal length 10cm lying in a uniform magnetic field B of magnitude 1.2T parallel to its principal axis.A particle havig a charge 2.0×10−3C and mass 2.0×10−5kg is projected perpendicular to the plane of the diagram with a speed of 4.8m/s.The particle moves along a circle with its centre on the principal axis at a distance of 15cm from the lens.The axis of the lens and of the circle are same.Show that the image of the particle goes along a circle and find the radius of that circle.
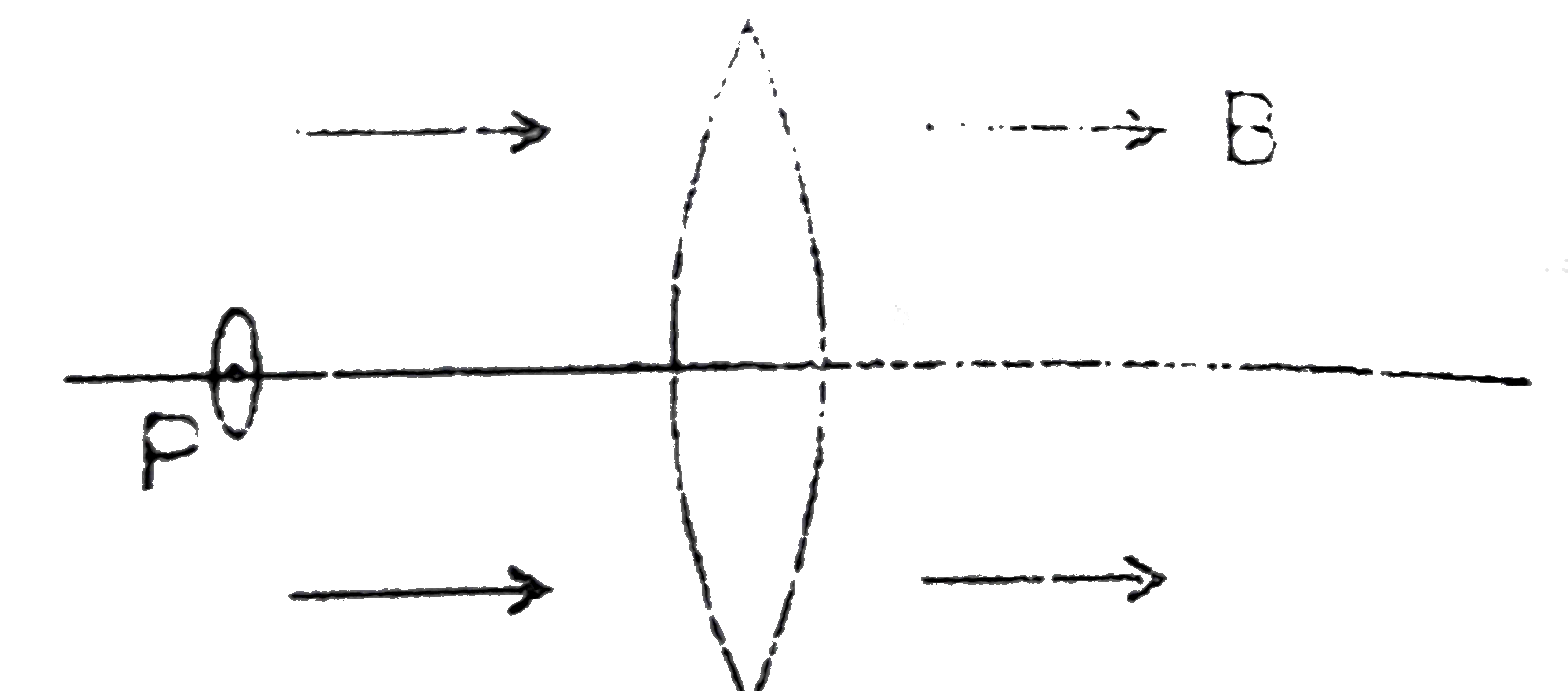 View Solution
View SolutionThe hinge of door is at a distance of 40 cm from the point of application of force. If a force of 20 N is applied, what is the magnitude of moment of force ?
View SolutionIn figure the uniform gate weights 300N and is 3m wide &2m high. It is supported by a hinge at the bottom left corner and a horizontal cable at the top left corner, as shown. Find :
(a) the tension in the cable and
(b) the force that the hinge exerts on the gate ( magnitude & direction ).
 View Solution
View SolutionTake the mean distance of the moon and the sun from the earth to be0.4×106km and 150×106km respectively. Their masses are 8×1022kg and 2×1030kg respectively. The radius of the earth of is 6400km. Let ΔF1be the difference in the forces exerted by the moon at the nearest and farthest points on the earth and ΔF2 be the difference in the force exerted b the sun at the nearest and farthest points on the earth. Then, the number closest to ΔF1ΔF2 is :
View SolutionThe magnitude of torque on a particle of mass 1 kg is 2.5 Nm about the origin.If the force acting it is 1 N, and the distance of the particle from the origin is 5 m, the angle between the force and the position vector is (in radians):
View SolutionOne end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A.Find the magnitude of the tension T in the string and force F.
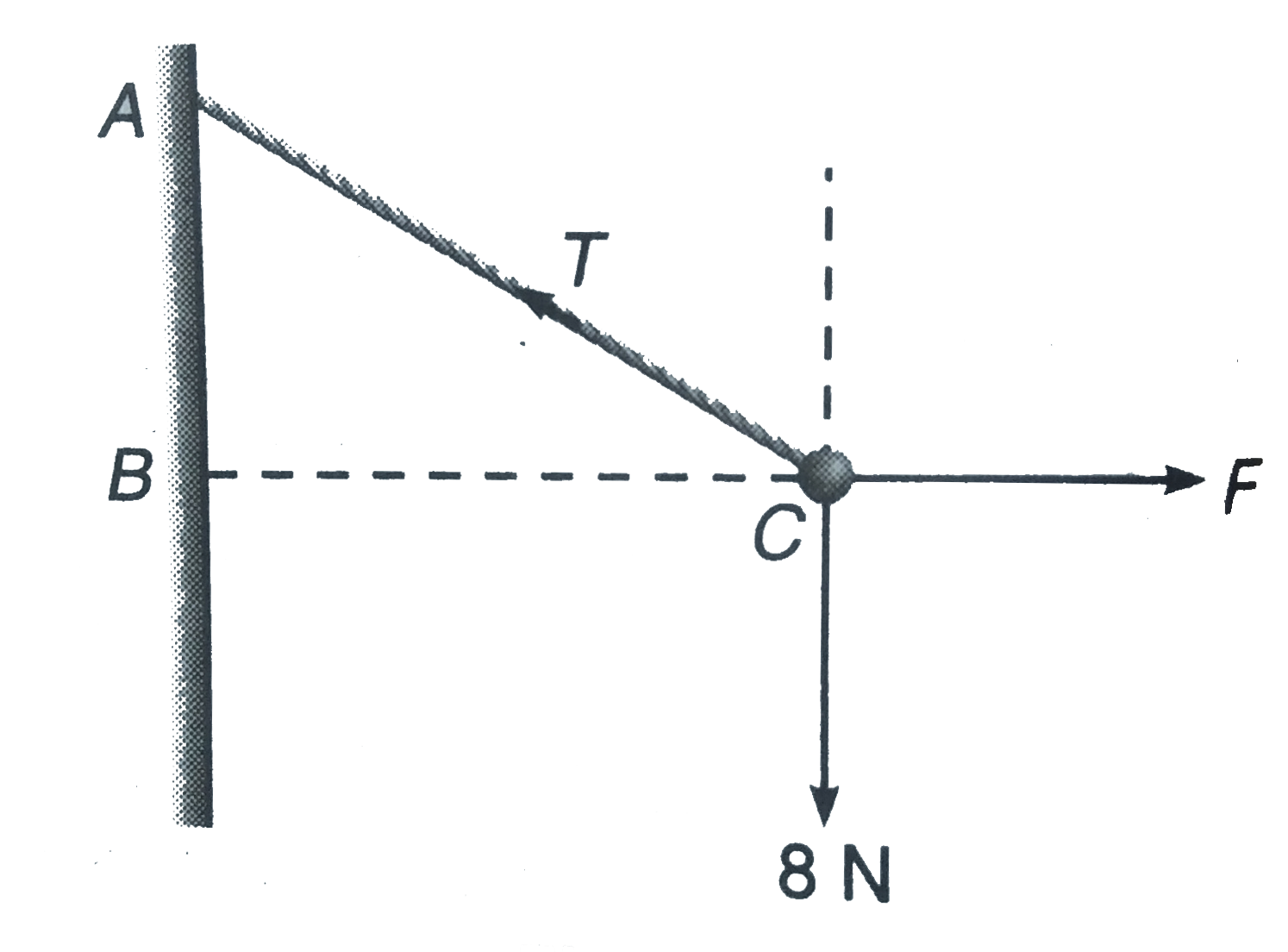 View Solution
View Solution
