The centre of mass of a non uniform rod of length L, whose mass per unit length varies as ρ=k.x2L where k is a constant and x is the distance of any point from one end is (from the same end)
Let the x-axis be along the length of the rod and origin at one of its ends. As rod is along x-axis, for all points on it y and z co - ordinates are zero.
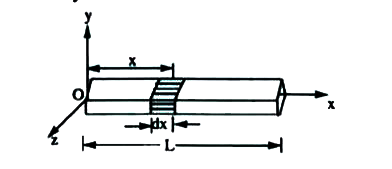
Centre of mass will be on the rod. Now consider an element of rod of length dx at a distance x from the origin, then dm=λdx=Kx2Ldx, so,
XCM=∫L0xdm∫L0dm=∫L0xkx2Ldx∫L0kx2Ldx=∫L0x3dx∫L0x2dx=l44L33=3L4
Similar Questions
The centre of mass of a non-uniform rod of length L whose mass per unit length λ is proportional to x2, where x is distance from one end
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View Solution
Knowledge Check
The density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be atA3(2+b)4(3+b)B4(2+b)3(3+b)C3(3+b)4(2+b)D4(3+b)3(2+b)
The density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be at
View SolutionThe liner density of a rod of length 2m varies as λ=(2+3x) kg/m, where x is distance from end A . The distance of a center of mass from the end B will be
_PHY_E05_180_Q02.png)
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA rod of length L is of non uniform cross-section. Its mass per unit length varies linearly with distance from left end. Then its centre of mass from left end is at a distance. (Take linear density at left end=0).
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View Solution