A 2kg block is connected with two springs of force constants K1=100NmandK2=300Nm as show in figure. The block is released from rest with the springs unstreched. Find the acceleration of the block in its lowest position (g=10m/s2)
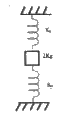
Let .x. be the maximum displacement of block downwards. Then from conservation of mechanical energy : decrease in potential energy of 2 kg block = increase in elastic potential energy of both the springs
∴mgx=12(k1+k2)x2
or x=2mgk1+k2=(2)(2)(10)100+300=0.1m
Acceleration of block in this position is
a=(k1+k2)x−mgm (upwards)
=(400)(0.1)−(2)(10)2=10m/s2 upwards
Similar Questions
A 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

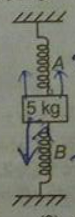
View SolutionA 5 kg block in connected with two spring A and B having force constant, K1=200Nm and K2=300Nm respectively as shown in the figure . The block is released from rest with both the springs in natural length. The maximum energy stored in the spring A will be
View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
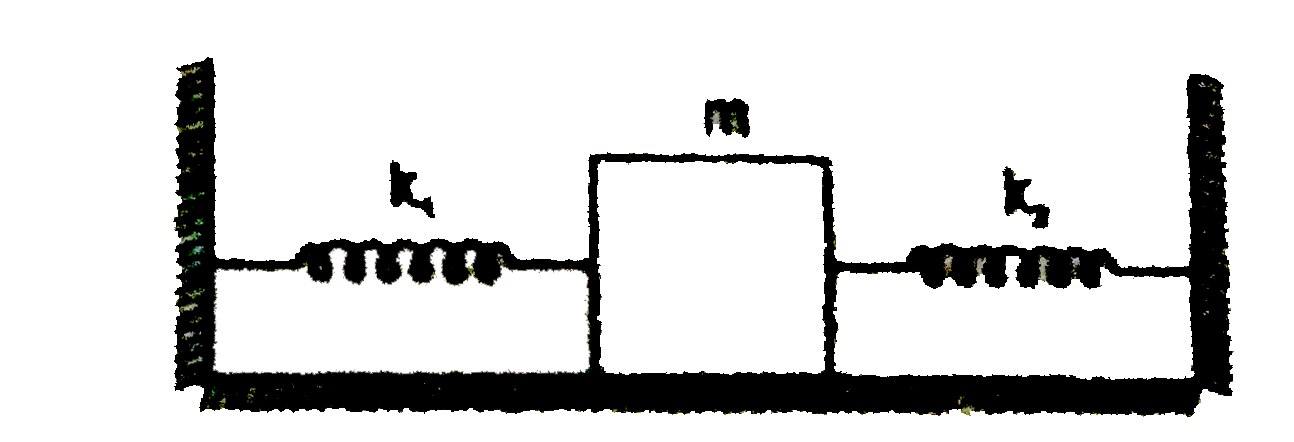
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
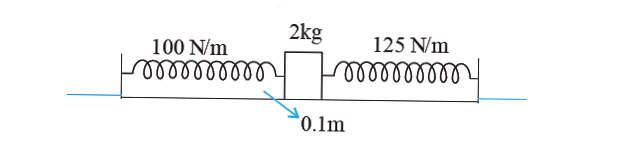
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
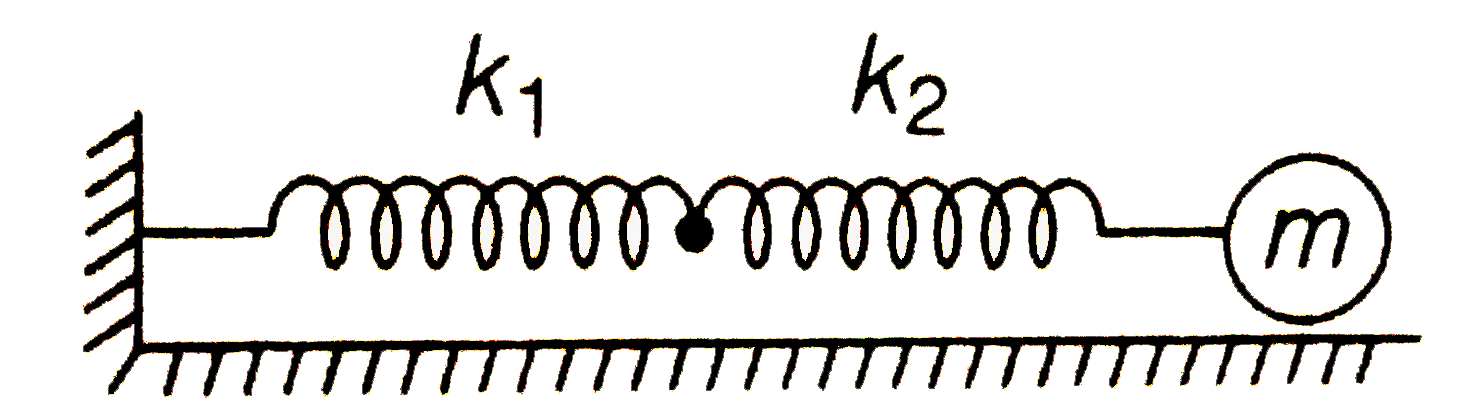
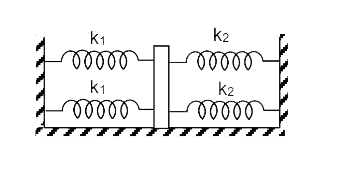
View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
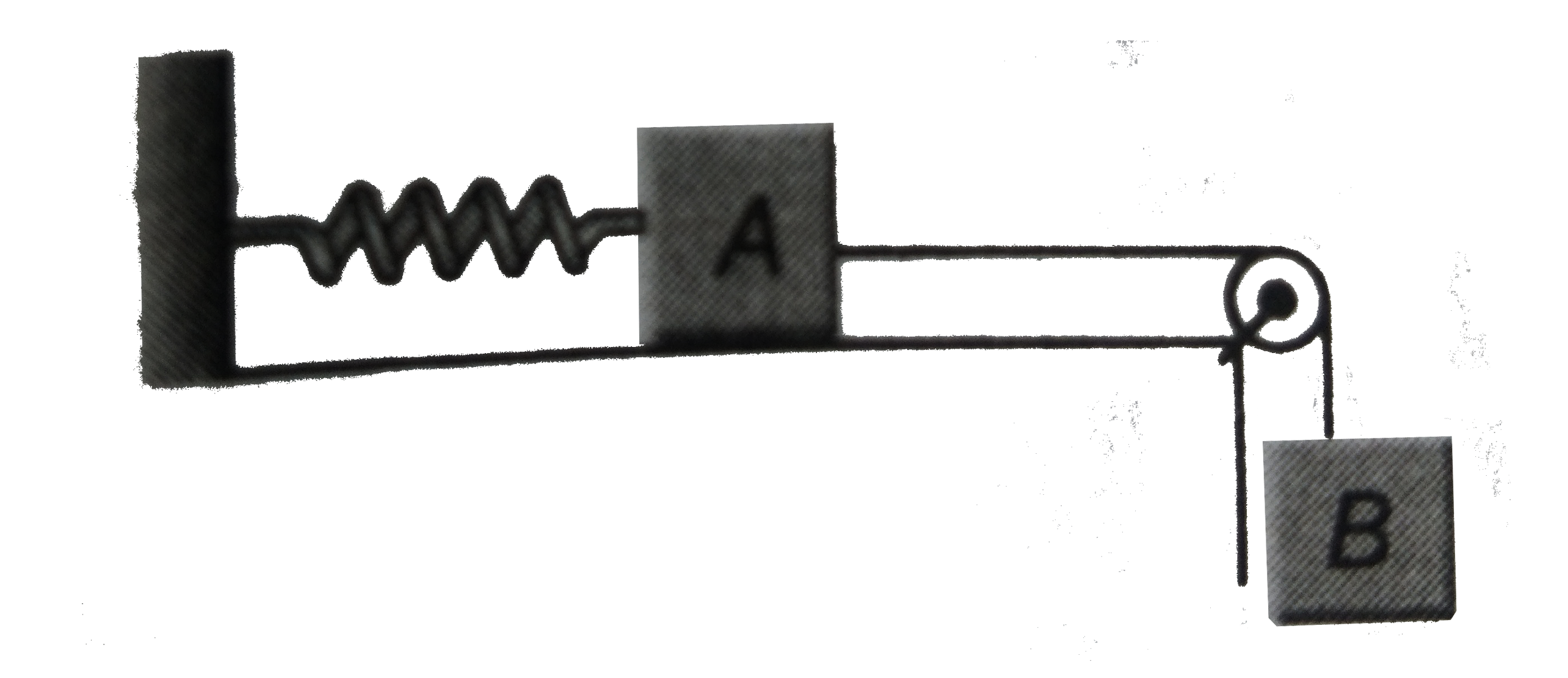 .
.
View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View Solution
