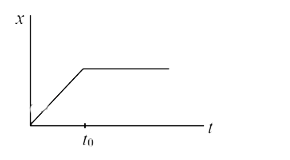
Figure 3.21 shows the x−t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t<0 and on a parabolic path for t>0 ? If not, suggest a suitable physical context for this graph.
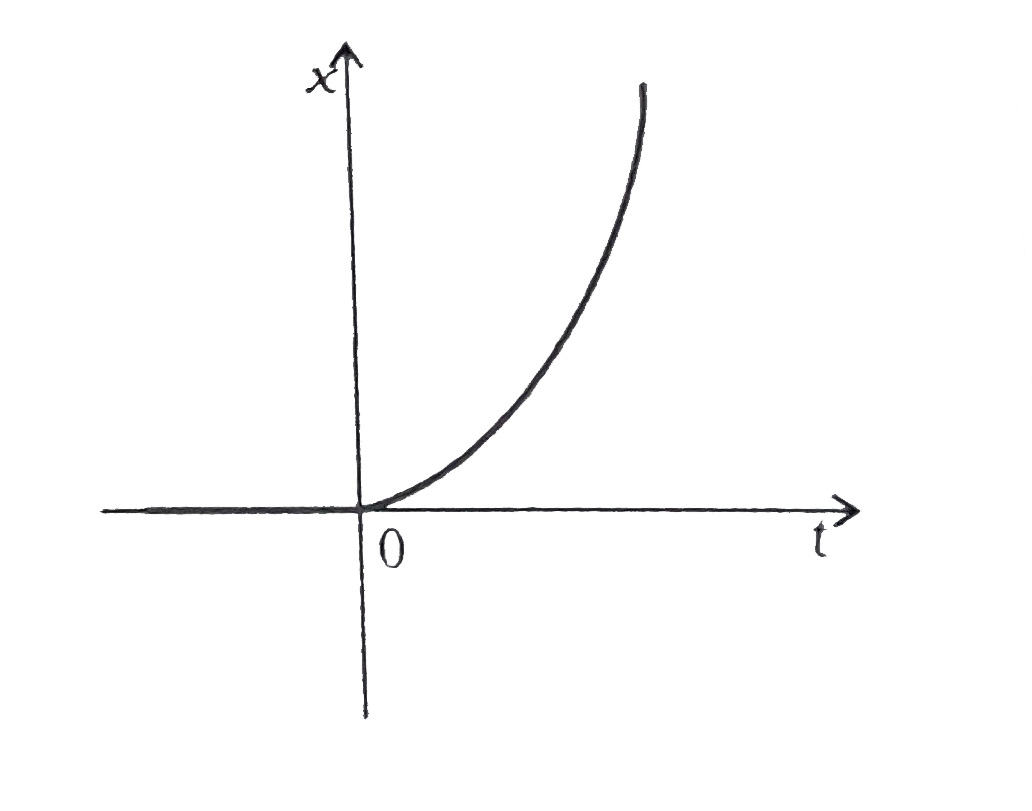
It is not correct to say that the particle moves in a straight line for t<0, (i.e, -ve) and on a parabolic path for t>0 (i.e, +ve) because the x-t graph can not show the path of the particle.
For the graph a suitable physical contxt can be the particle thrown from the top of a tower at the instant t=0.
Similar Questions
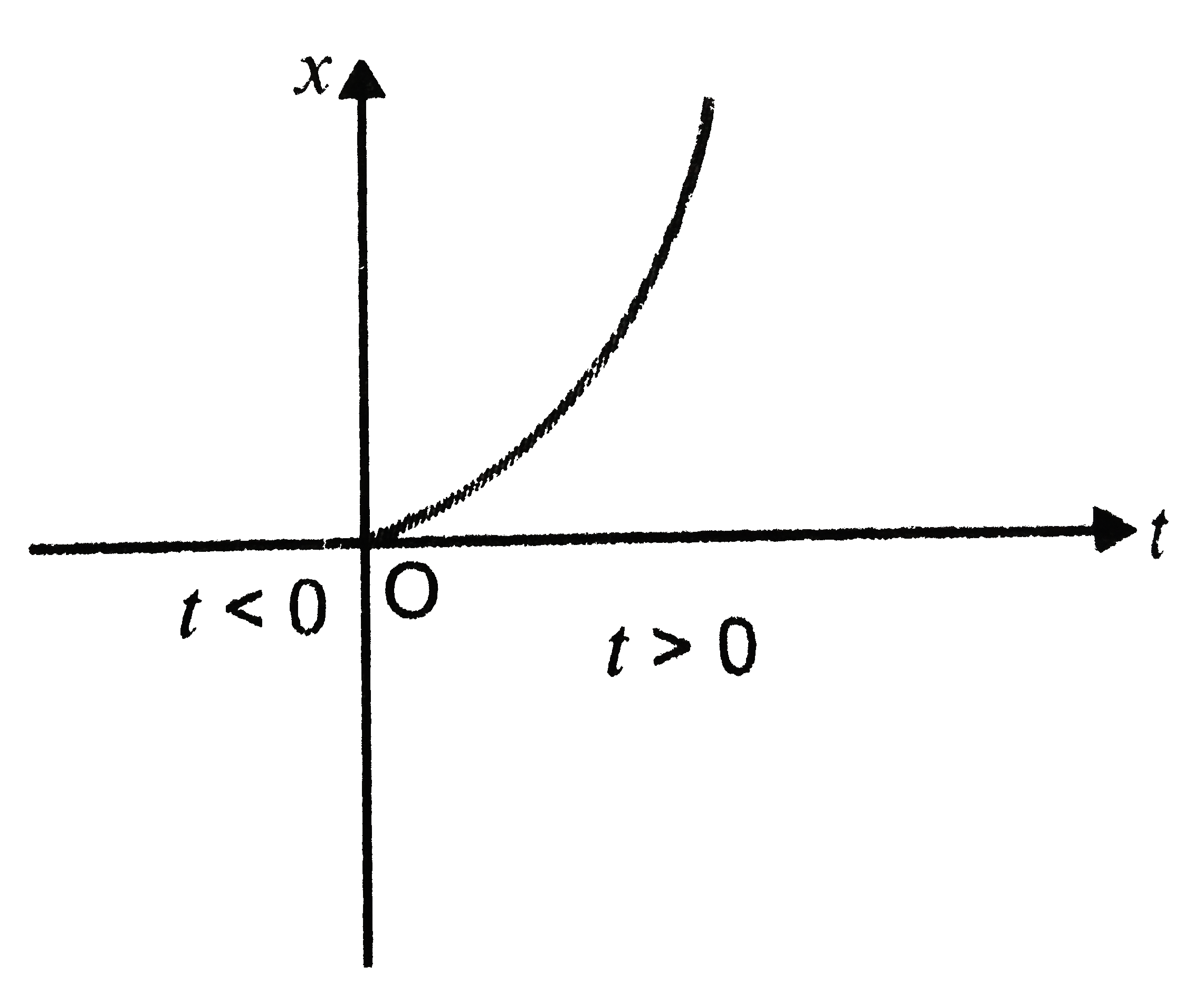
Fig. shows x−t plot of one dimensional motion a particle. Is it correct to say from the graph that the particle moves in a straight line for t<0 and on a parabolic path form t>0? If not, suggest a suitable physical context for this graph.
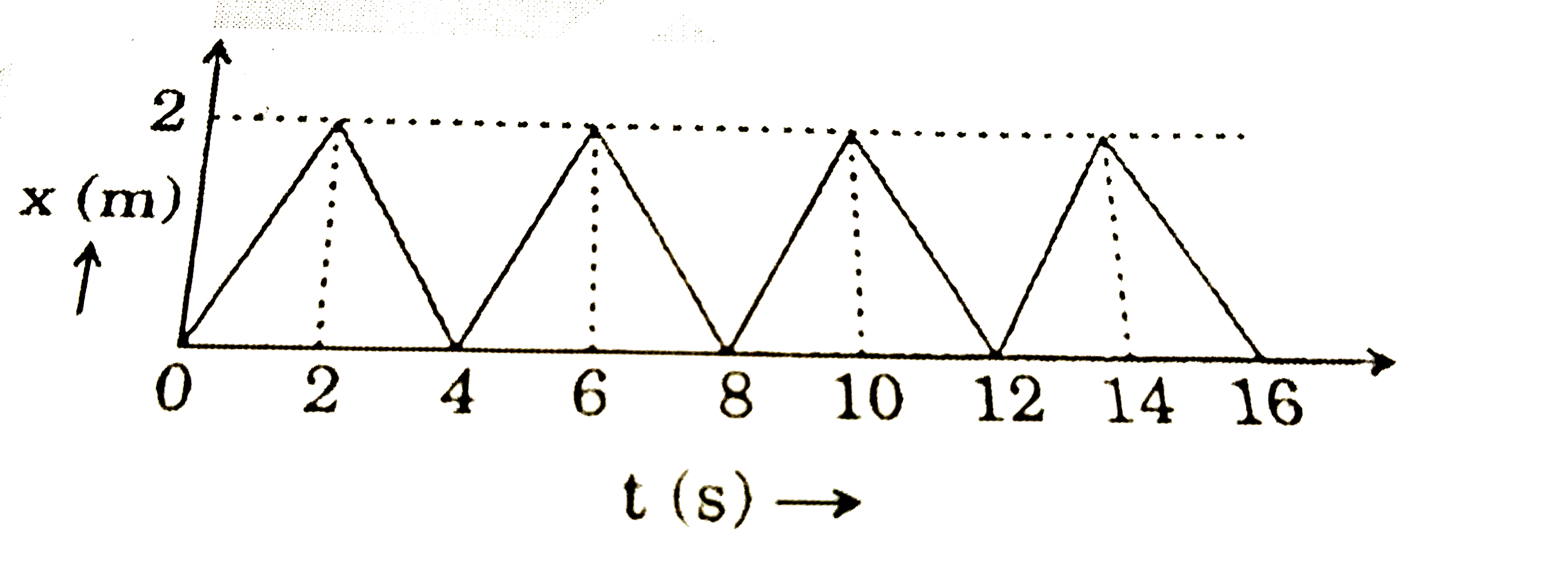
View SolutionThe figure shows the position - time (x - t) graph of one-dimensional motion of a body of mass 0.4 kg. The magnetic of each impulse is
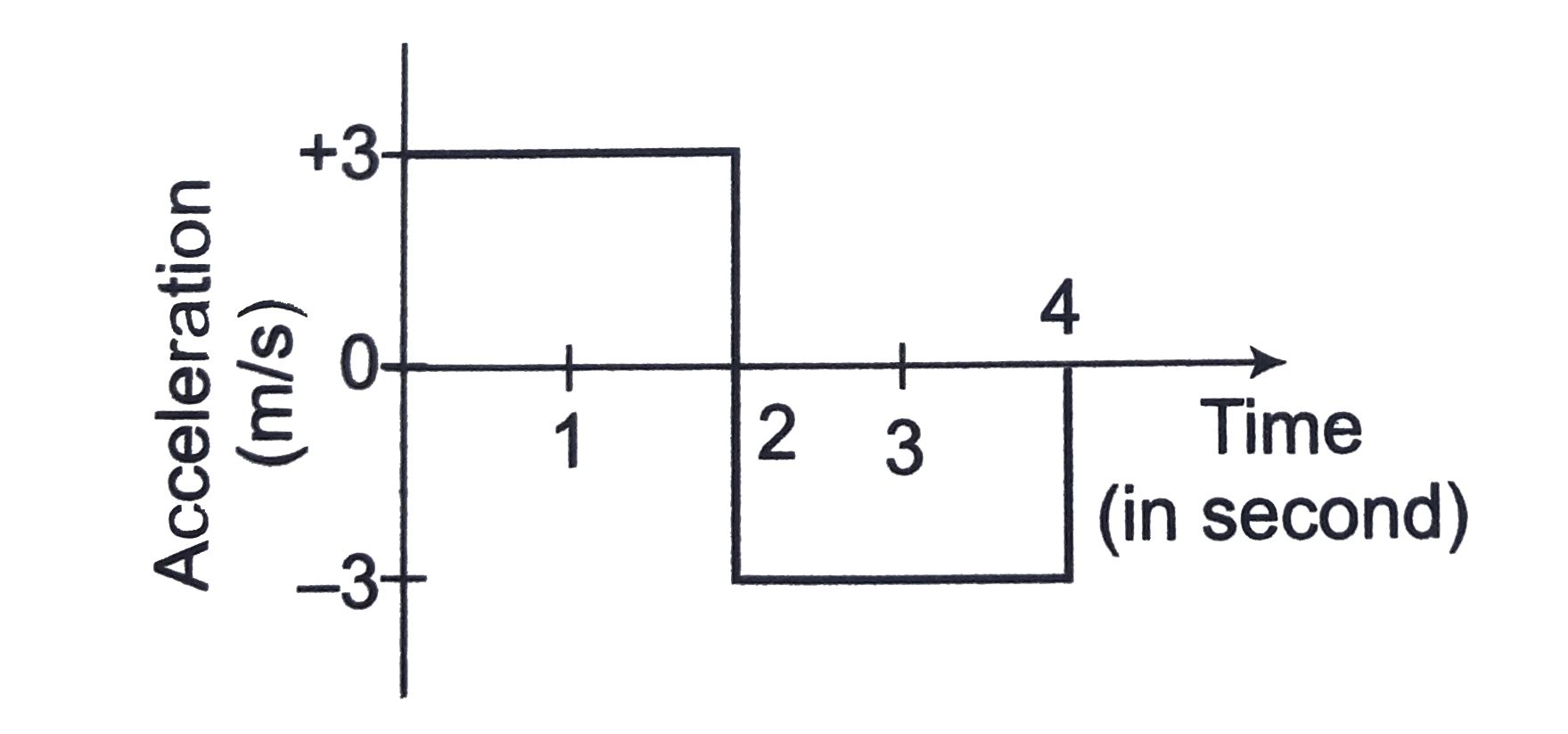
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
View SolutionThe fig. shows the v−t graph of a particle moving in straight line. Find the time when particle returns to the starting point.
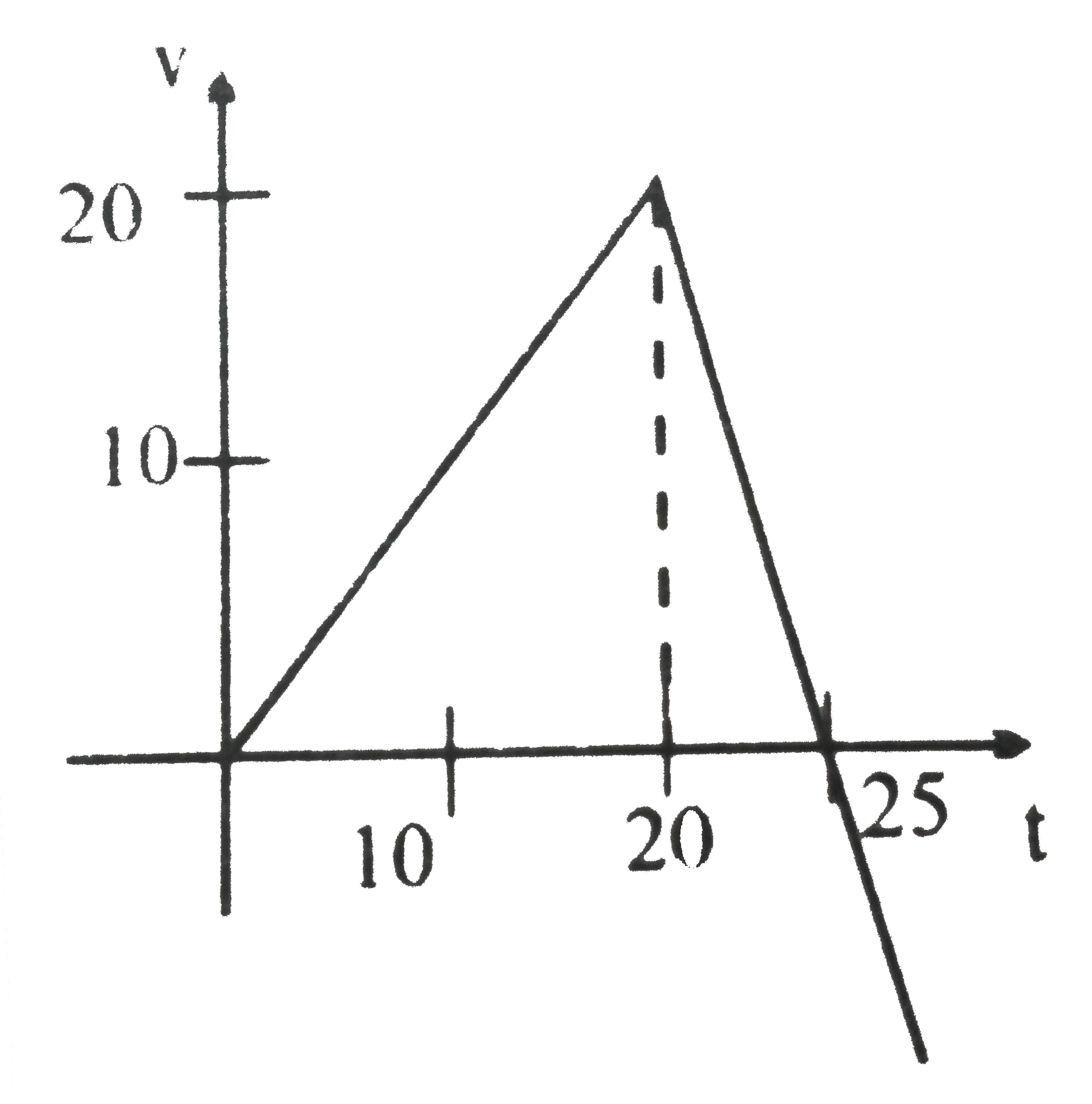
View SolutionFigure below shows the velocity-time graph of a one dimensional motion. Which of the following characteristic of the particle is represented by the shaded area?

View SolutionThe velovity-time graph of a particle moving in a straitht line is shown in . The acceleration of the particle at t=9s is.
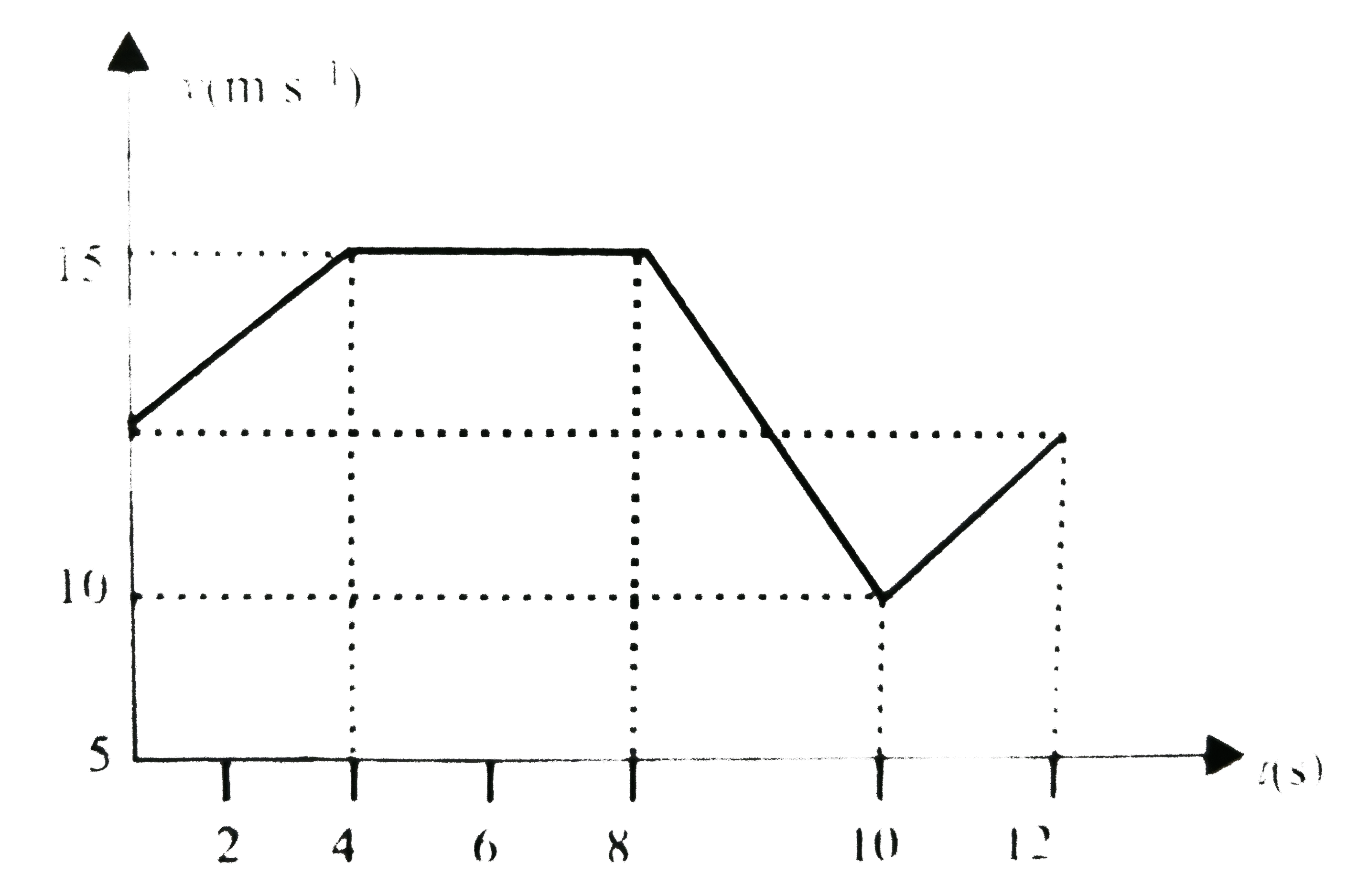 .
.
View SolutionFigure shows the position-time graph of a particle moving on the X--axis. Which of these option correctly describes the particle 's motion?
View SolutionThe velocity time graph of a particle moving in a straight line is given line is given in the figure. Then starting from t=0, the particle
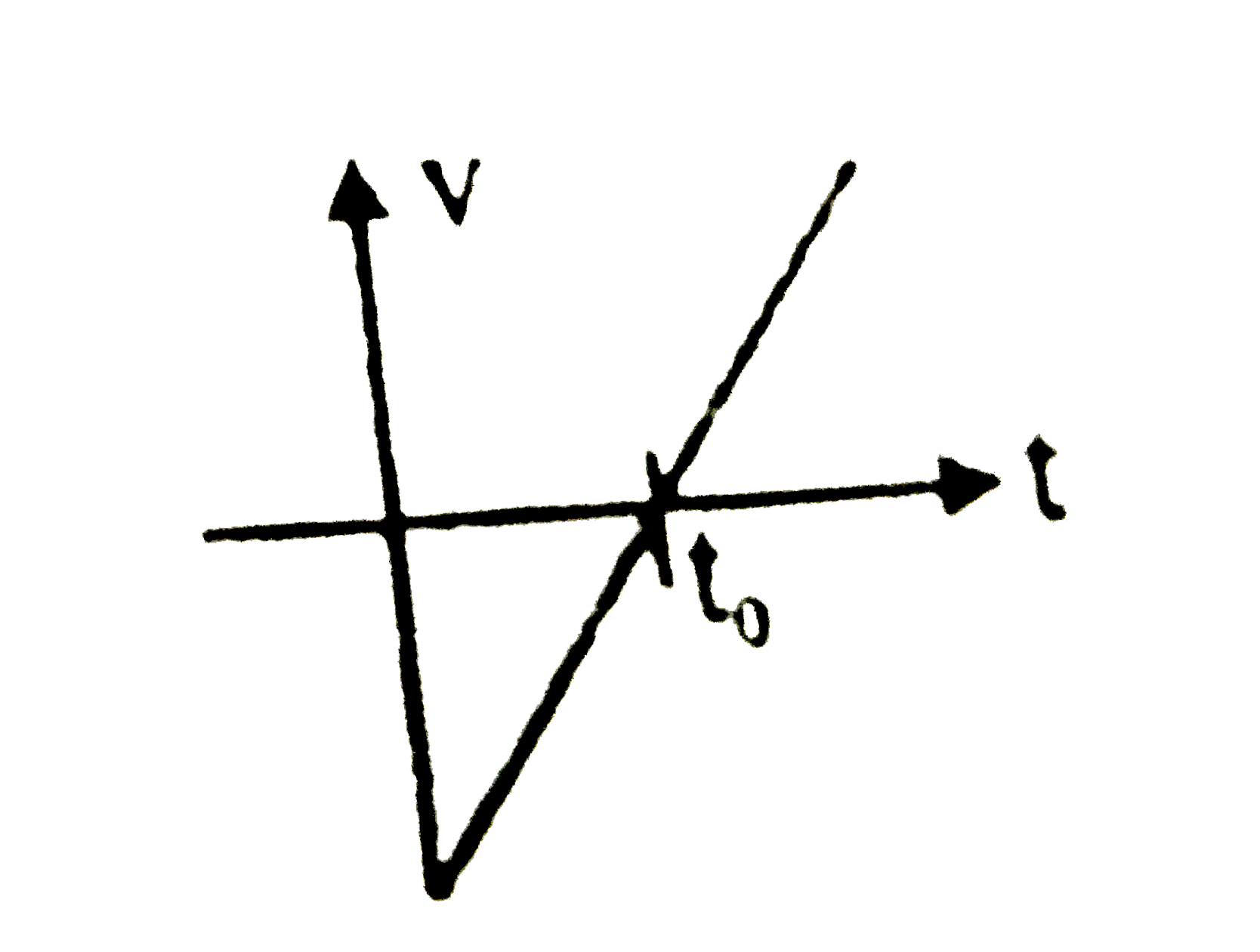
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−
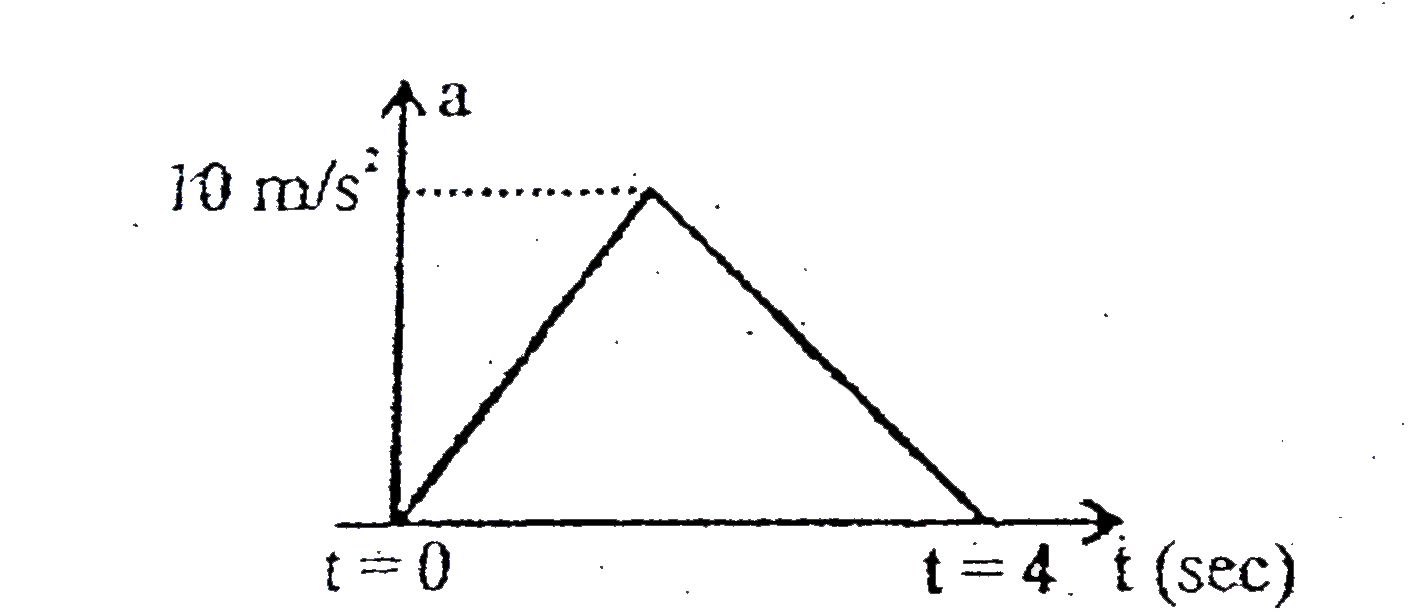
View SolutionThe figure shows the v−t graph of a particle moving in a straight line. Starting from rest, the time after which the particle returns to its starting position is
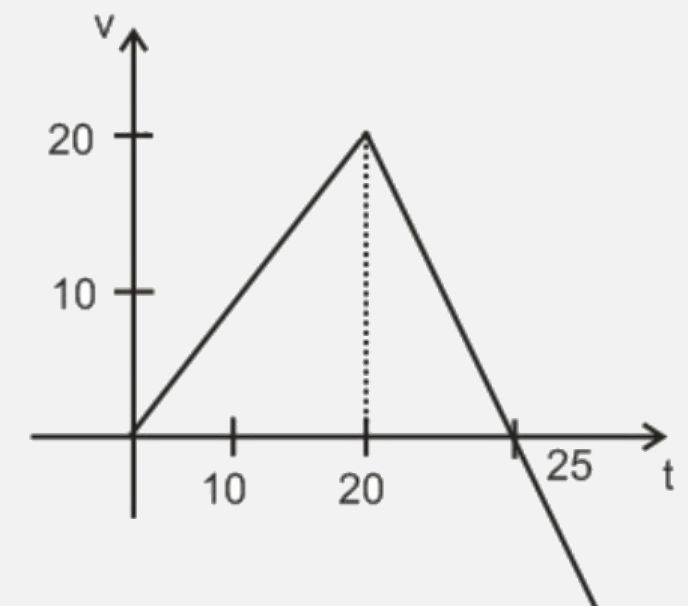
View Solution
