The pulley A and C are fixed while the pulley B is movable. A mass M2 is attached to pulley B , while the string has masses M1andM3 at the two ends. Find the acceleration of each mass .
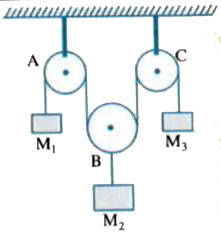
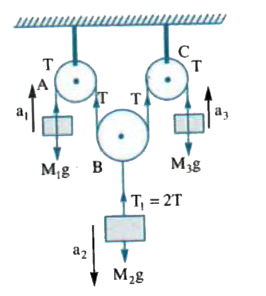
The force acting on masses M1,M2andM3 are shown in figure .
Let a2anda3 be upward acceleration of masses M1andM3anda2 the downward acceleration of mass M2 .
For motion of mass M1
T−M1g=M1a1....... (1)
For motion of mass M3
T−M3g=M3a3 ........ (2)
For motion of mass M2
M2g−2T=M2a2 ......... (3)
Let l1,l2,l3 be the lengths of vertical portions of the string between pulley at any instant. M1 goes up through x,M2 goes down through y and M3 goes up through z.
Then l1+2l2+l3=(l1−x)+2(l2+y)+l3−z
⇒x+z=2y⇒d2xdt2+d2zdt2=2d2ydt2
a1+a3=2a2⇒a2=a1+a32.......... (4)
From (1) , a1=TM1−g ....... (5)
From (2) ,a3=TM3−g ............ (6)
substituting a1anda3 is (4) , we get
a2=T2(1M1+1M3)−g......... (7)
From (3) , T=M2(g−a2)2 .......... (8)
substituting this value in (7) , we get
a2=M24(g−a2)(1M1+1M3)−gora2=M2(g−a2)(M3+M1)4M1M3−g
or4M1M3a2_M2(M1+M3)g−M2(M1+M3)a2−4M1M3g
or[4M1M3+M2(M1+M3)]a2=(M1+M3)M2g−4M1M3g
a2=(M1+M3)M2g−4M1M3g4M1M3+M2(M1+M3) a2=M1M2+M2M3−4M1M3M1M2+M2M3+4M1M3g...... (9)
substituting value of T from (8) in (5)
a1=M2(g−a2)2M1−g
Substituting value of a2 in above equation , we get
a1=−M1M−2+3M2M3−4M1M3M1M2+M2M3+4M1M3g ........ (10)
Similarly from (6) and (9)
a3=3M1M2−M2M3−4M1M3M1M2+M2M3−4M1M3 ........ (11)
Similar Questions
Two block of masses m=5kgandM=10kg are connected by a string passing over a pulley B as shown. Another string connect the center of pulley B to the floor and passes over another pulley A as shown. An upwards force F is applied at the center of pulley A. Both the pulleys are massless.
Find the acceleration of block m and M, if F is
(a) 100N
(b)300N
(c)500N(Takeg=10m/s2)

View SolutionIf the string & all the pulleys are ideal, acceleration of mass m is :-
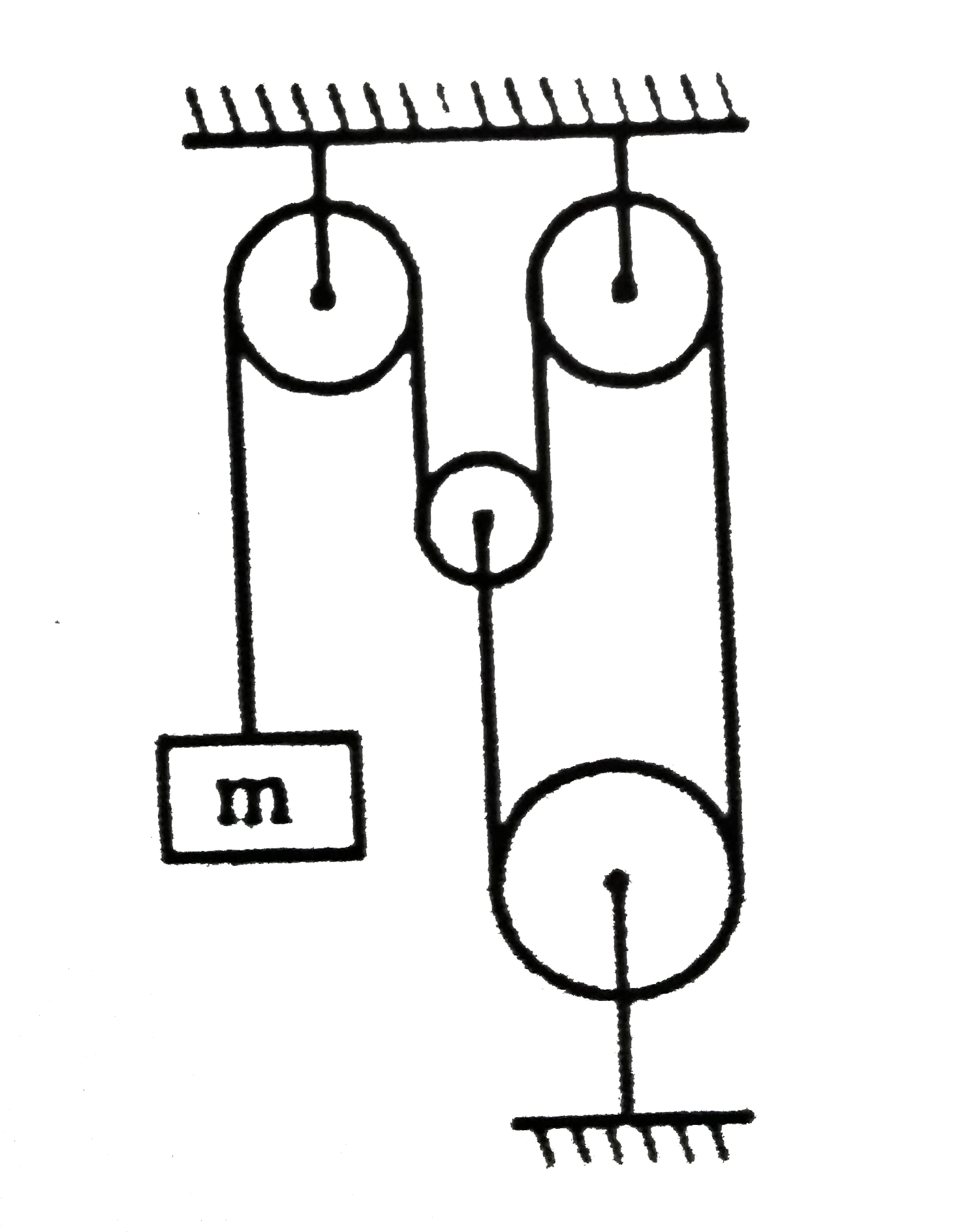
View Solution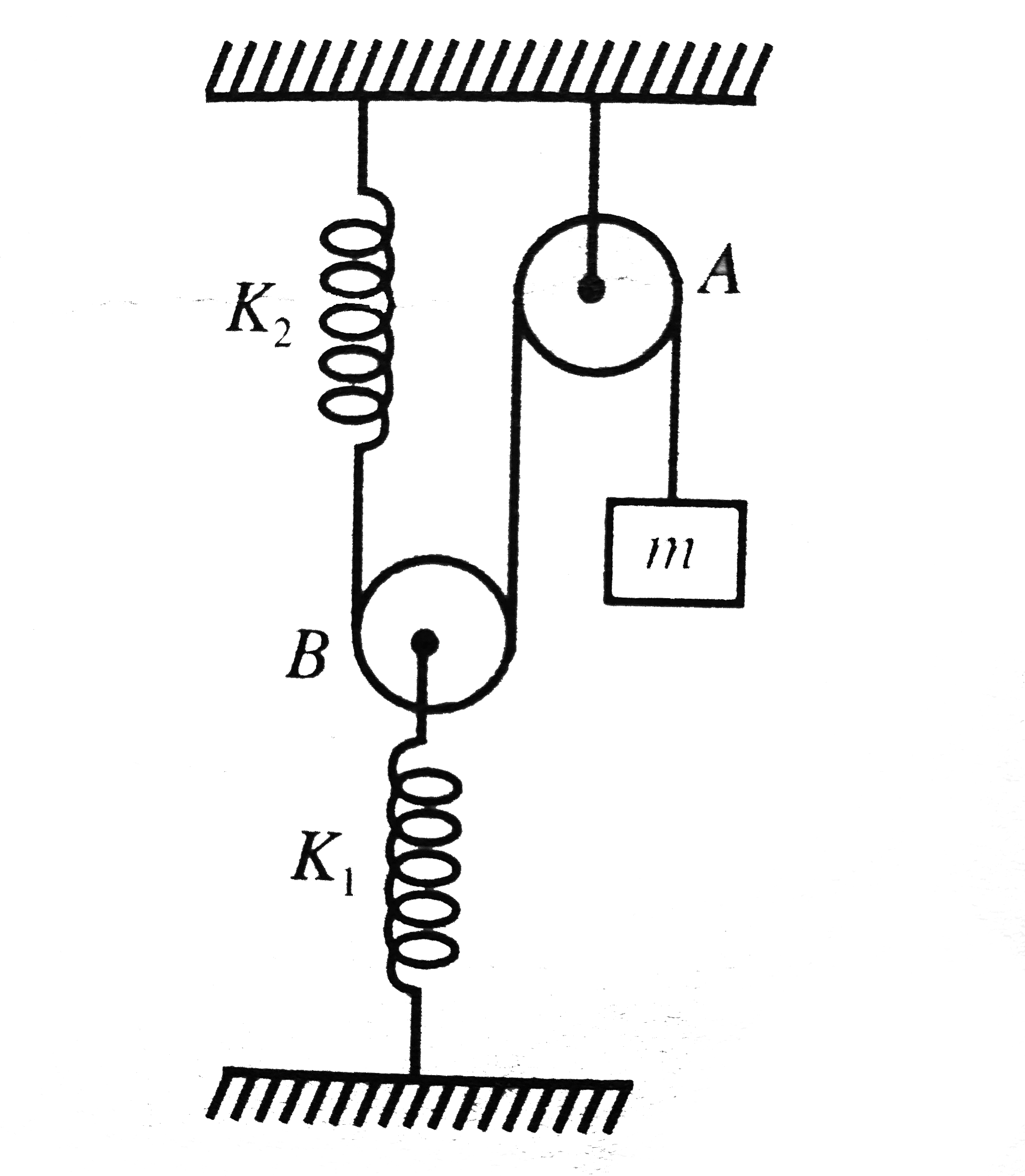
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View SolutionA smooth pulley A of mass M0 is lying on a frictionless table. A massless rope passes round the pulley and has masses M1 and M2 tied to its ends, the two portions of the string being perpendicular to the edge of the table so that the masses hang vertically. Find the acceleration of the pulley.
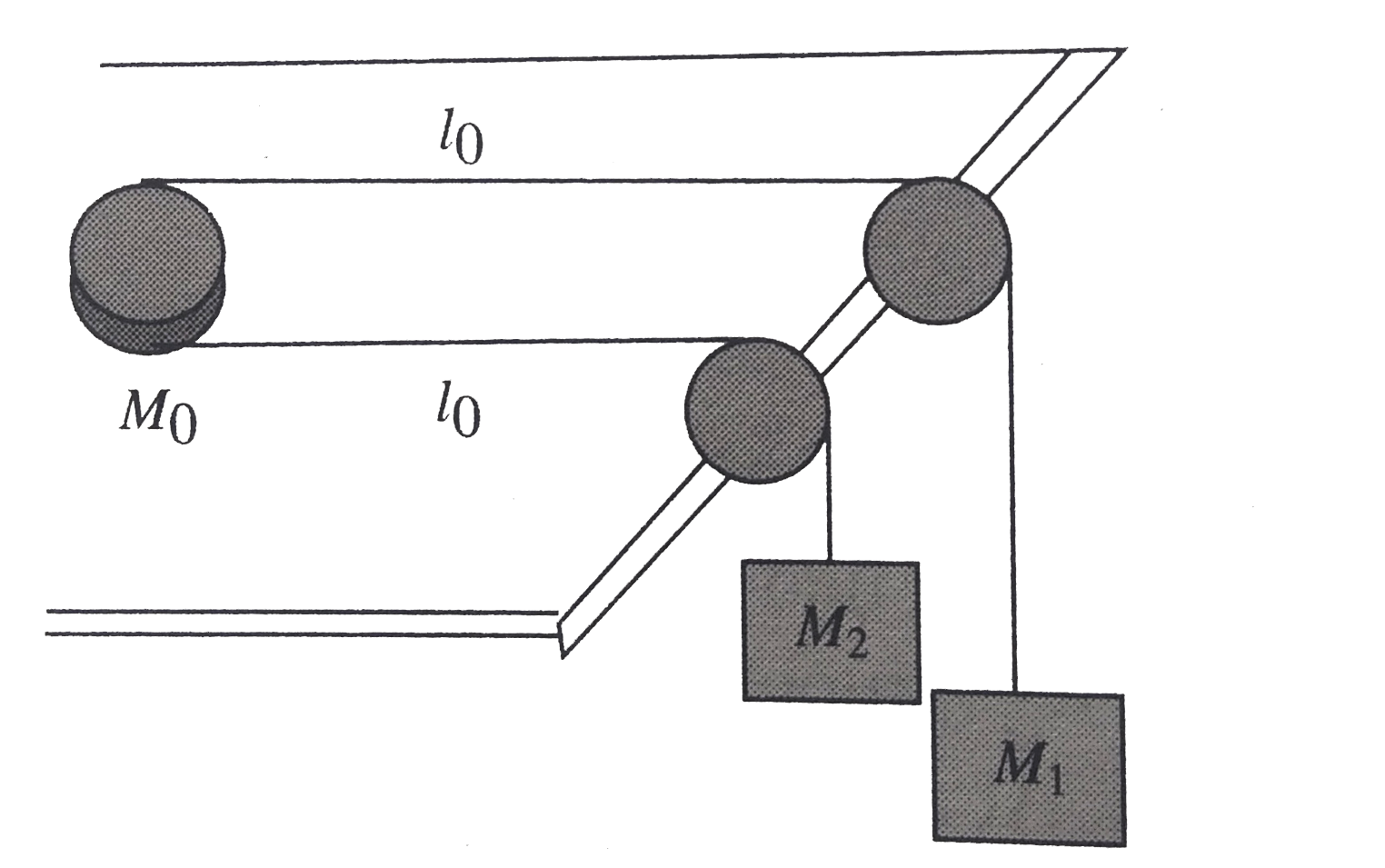
View SolutionA block A of mass m is tied to a fixed point C on a horizontal table through a string passing round a massless smooth pulley B. A force F is applied by the experimenter to the pulley. Show that if the pulley is displaced by a distance x the block will be displaced by 2x. Find the acceleration of the block and the pulley.

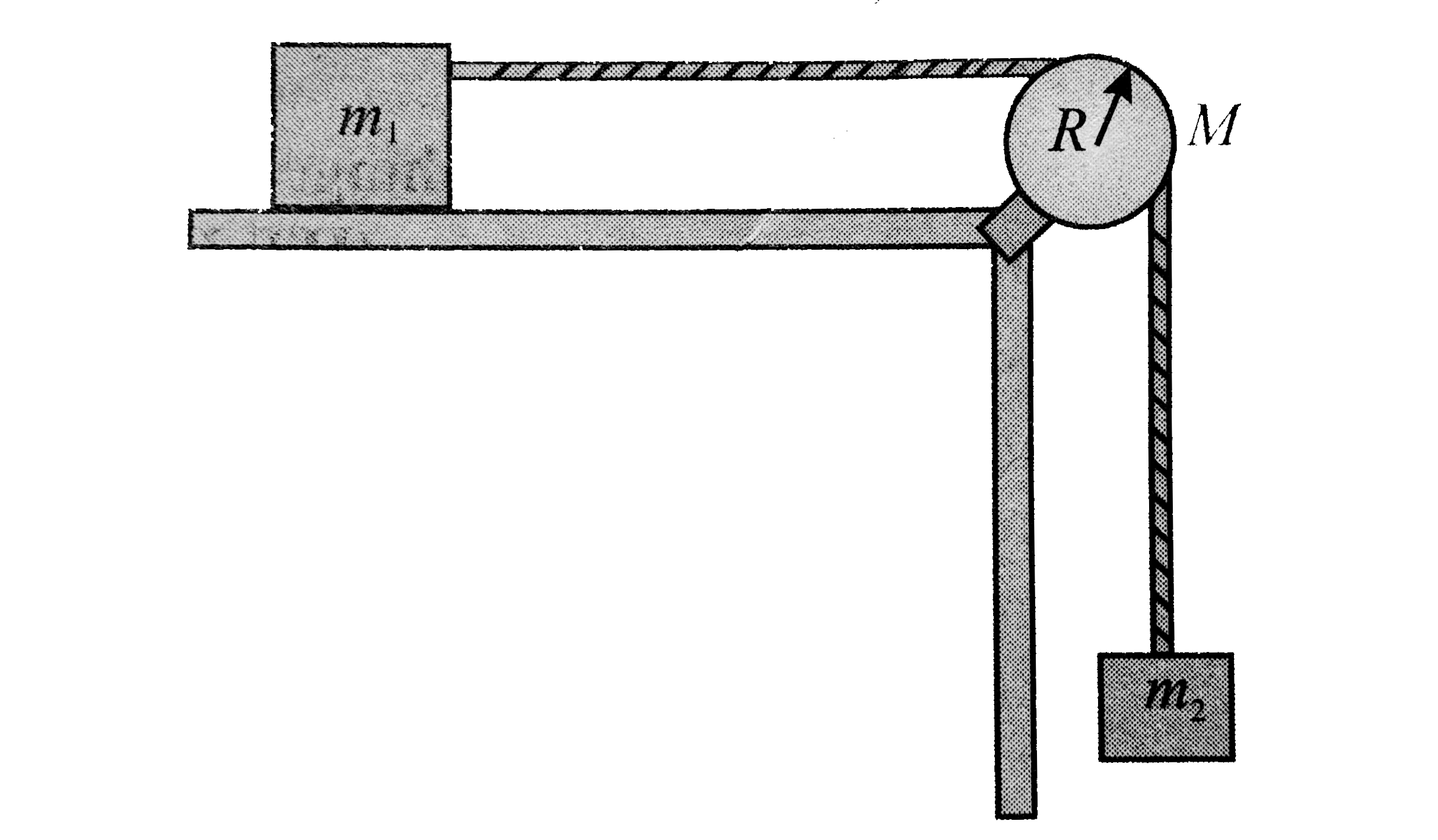
View SolutionIn figure mass m1 slides without friction on the horizontal surface, the frictionless pulley is in the form of a cylinder of mass M and radius R, and a string turns the pulley without slipping. Find the acceleration of each mass, and tension in each part of the string.
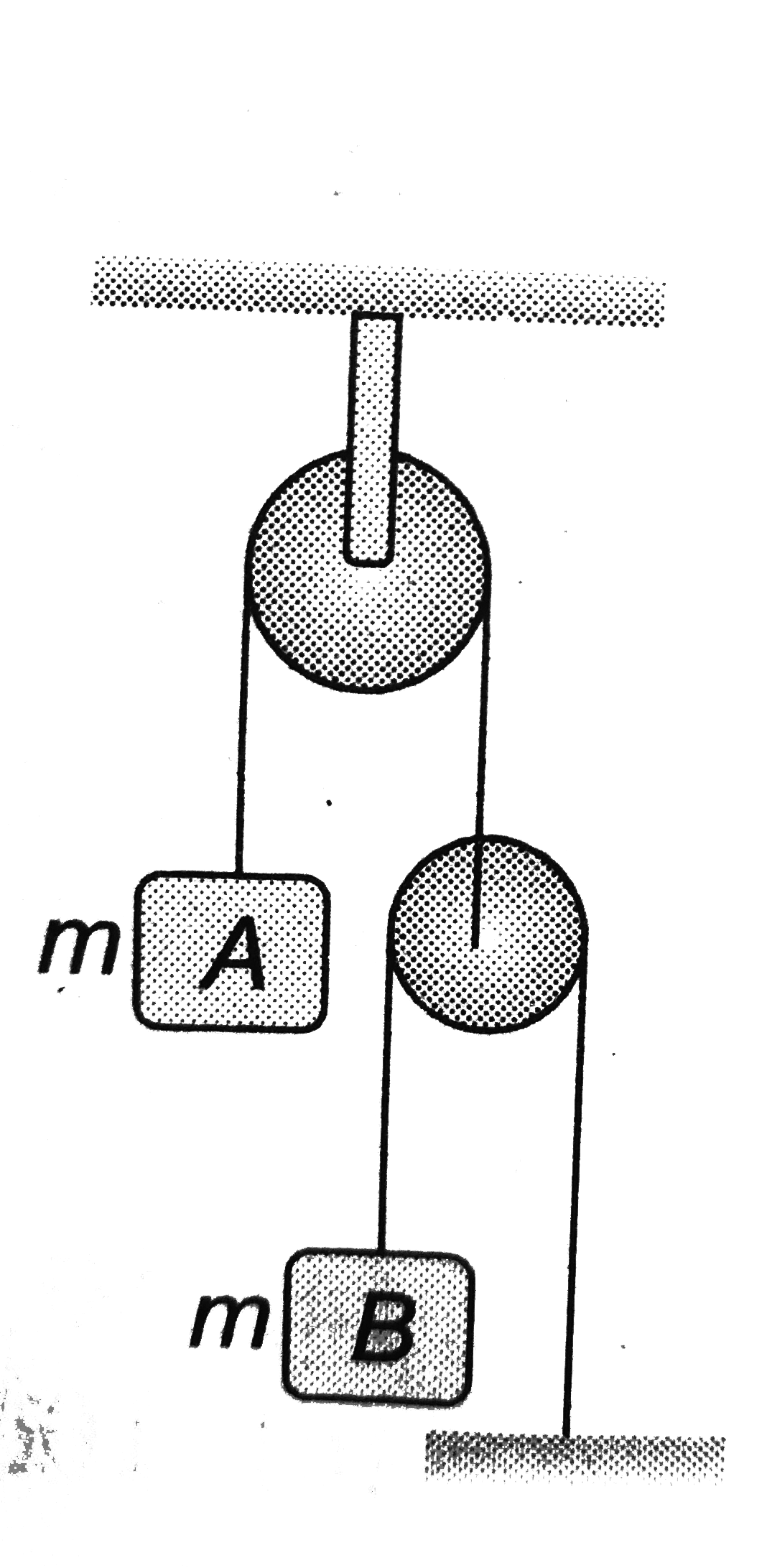
View SolutionIn the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
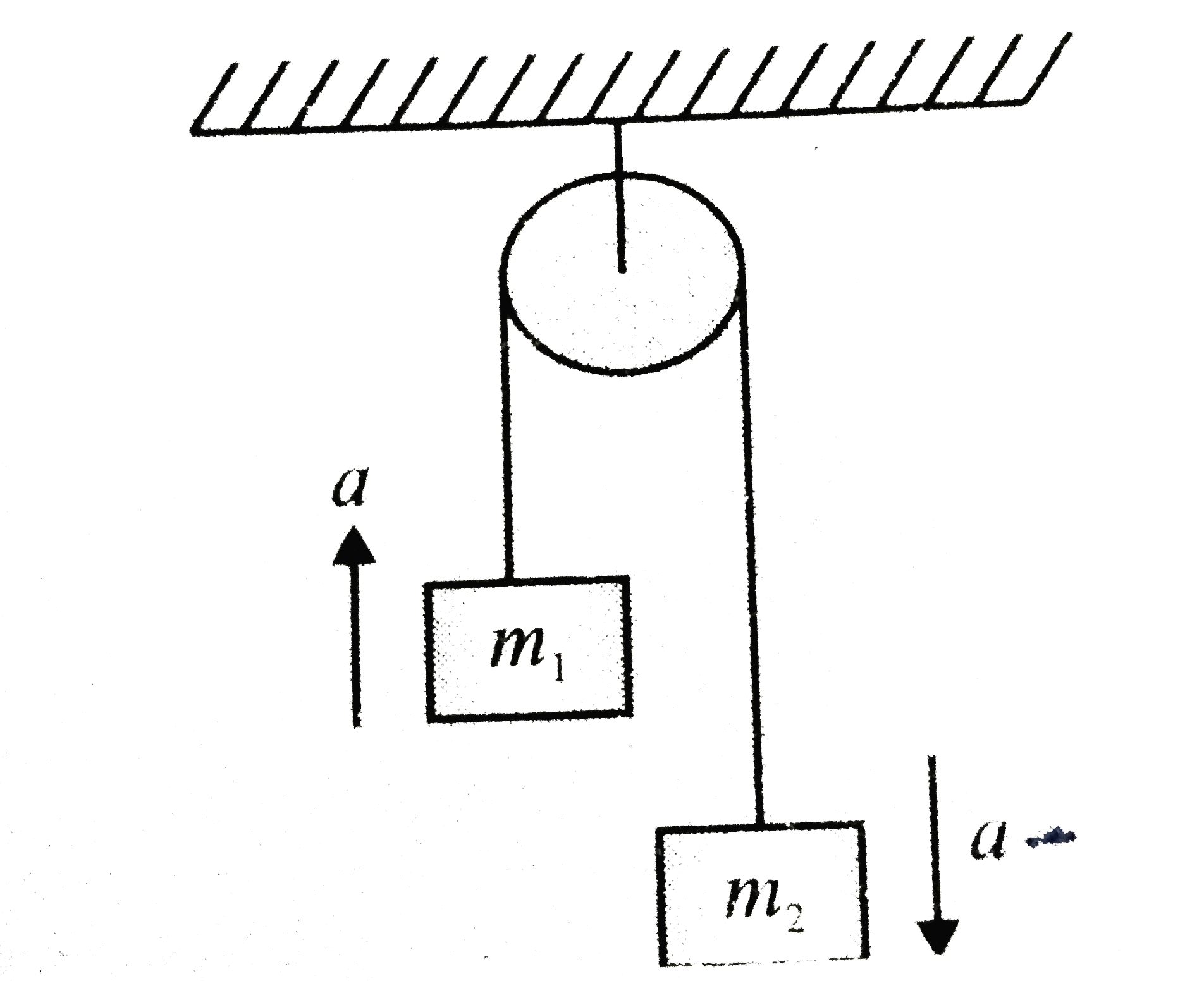
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the masses m1andm2. The car starts going up with an acceleration a0. Assuming the masses of the pulley and the thread as well as the friction to be negligible, find:
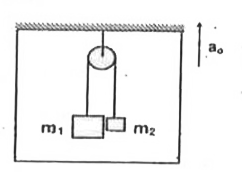
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car
(b) the force exerted by the pulley on the ceiling of the car. Given m1>m2.
View Solution
