n identical cubes each of amss m an side I are on the horizontal surface. Then the minimum amount of work done to arrange then one on the ther is
nmmgl
mgln22
mgln(n−1)2
mgln(n+1)2
The correct Answer is:C
To solve the problem of finding the minimum amount of work done to arrange n identical cubes, each of mass m and side length l, one on top of the other, we can follow these steps:
1. Understanding the Setup:
We have n identical cubes, each with mass m and side length l, placed on a horizontal surface. We need to stack these cubes vertically.
2. Calculating Work Done for Each Cube:
- The first cube is already on the ground, so no work is needed to place it.
- The second cube needs to be lifted to a height of l. The work done W1 to lift it is given by:
W1=m⋅g⋅l
- The third cube needs to be lifted to a height of 2l. The work done W2 is:
W2=m⋅g⋅2l
- Continuing this pattern, the kth cube needs to be lifted to a height of (k−1)l, where k ranges from 1 to n.
3. Total Work Done:
- The total work done W to stack all n cubes is the sum of the work done for each cube:
W=W1+W2+W3+…+Wn−1
- This can be expressed as:
W=m⋅g⋅l+m⋅g⋅2l+m⋅g⋅3l+…+m⋅g⋅(n−1)l
4. Factoring Out Common Terms:
- We can factor out m⋅g⋅l:
W=m⋅g⋅l⋅(1+2+3+…+(n−1))
5. Using the Formula for the Sum of First n Natural Numbers:
- The sum of the first n−1 natural numbers is given by:
S=(n−1)n2
- Therefore, we can substitute this into our expression for W:
W=m⋅g⋅l⋅(n−1)n2
6. Final Expression for Work Done:
- Thus, the minimum amount of work done to arrange the cubes is:
W=m⋅g⋅l⋅(n−1)n2
Final Answer:
The minimum amount of work done to arrange n identical cubes, each of mass m and side l, one on top of the other is:
W=m⋅g⋅l⋅(n−1)n2
We have n identical cubes, each with mass m and side length l, placed on a horizontal surface. We need to stack these cubes vertically.
- The first cube is already on the ground, so no work is needed to place it.
- The second cube needs to be lifted to a height of l. The work done W1 to lift it is given by:
W1=m⋅g⋅l
- The third cube needs to be lifted to a height of 2l. The work done W2 is:
W2=m⋅g⋅2l
- Continuing this pattern, the kth cube needs to be lifted to a height of (k−1)l, where k ranges from 1 to n.
- The total work done W to stack all n cubes is the sum of the work done for each cube:
W=W1+W2+W3+…+Wn−1
- This can be expressed as:
W=m⋅g⋅l+m⋅g⋅2l+m⋅g⋅3l+…+m⋅g⋅(n−1)l
- We can factor out m⋅g⋅l:
W=m⋅g⋅l⋅(1+2+3+…+(n−1))
- The sum of the first n−1 natural numbers is given by:
S=(n−1)n2
- Therefore, we can substitute this into our expression for W:
W=m⋅g⋅l⋅(n−1)n2
- Thus, the minimum amount of work done to arrange the cubes is:
W=m⋅g⋅l⋅(n−1)n2
The minimum amount of work done to arrange n identical cubes, each of mass m and side l, one on top of the other is:
W=m⋅g⋅l⋅(n−1)n2
Similar Questions
Three identical cubes each of mass m are place on a smooth horizontal surface.A constant force F is applied on A as shown in the figure.The force on B applied by C is
View SolutionThree identical spheres each of radius .R. are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is
View SolutionA man carries a load of 5 kg on his head through a distance of 10 m. the minimum amount of work is done when he
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View SolutionA horizontal 50 N force acts on a 2 kg crate which is at rest on a smooth horizontal surface. At the instant the particle has gone 2 m, the rate at which the force is doing work is :
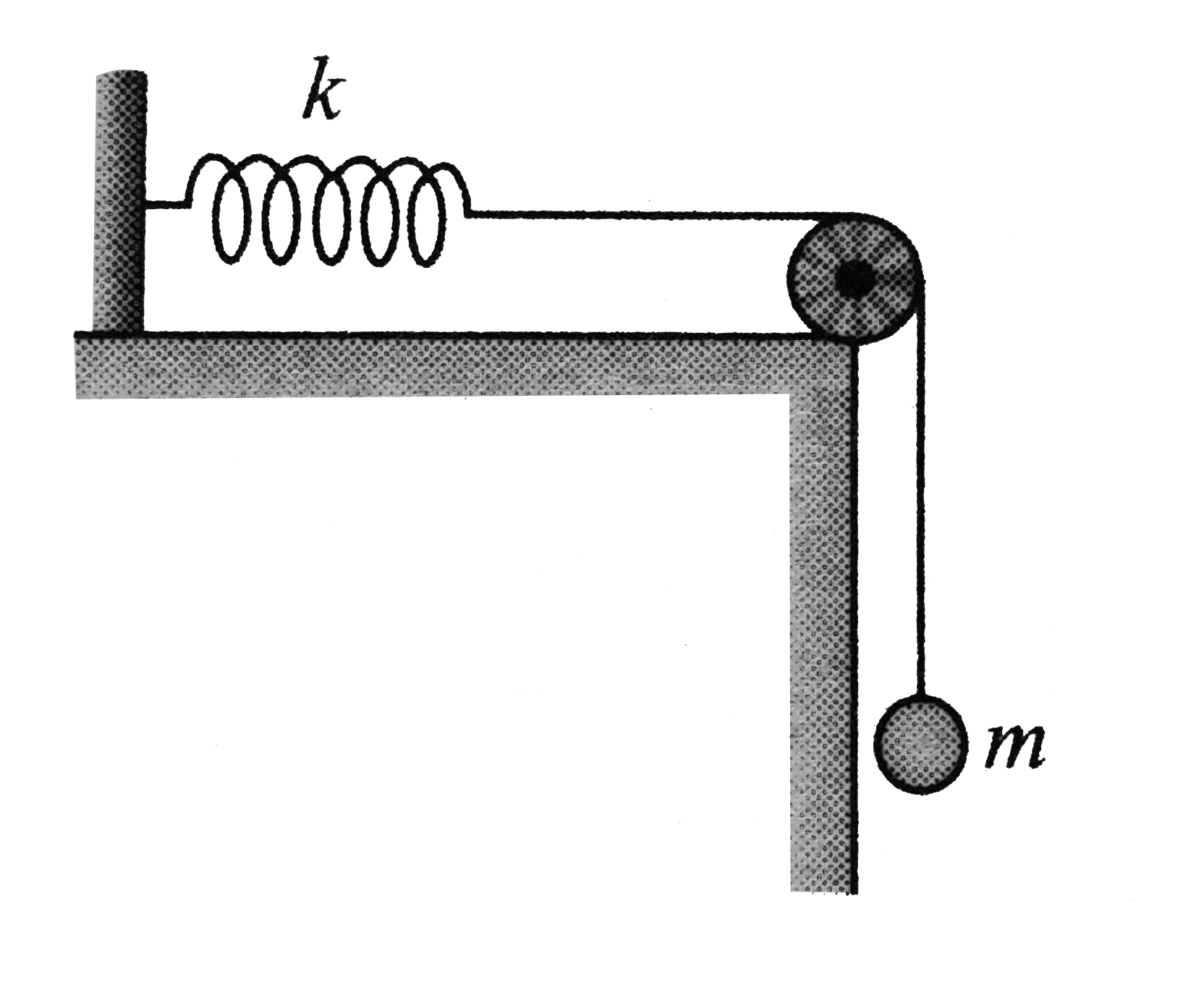
View SolutionIn figure, the light spring is of force constant k and is on a smooth horizontal surface. Initially the spring is relaxed. Calculate the work done by an external agent to lower the hanging body of mass M slowly, till it remains in equilibrium.
View SolutionThree cubes each of side 5cm are joined end to end. Find the surface area of the resulting cuboid.
View SolutionThree cubes each of side 5cm are joined end to end. Find the surface area of the resulting cuboid.
View SolutionThree cubes each of side 5cm are joined end to end. Find the surface area of the resulting cuboid.
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View Solution