n' identical cubes each of mass 'm' and edge 'L' are on a floor. If the cubes are to be arranged one over the other in a vertical stack, the work to be done is
Lmng(n−1)/2
Lg(n−1)/mn
(n−1)/Lmng
Lmng/2(n−1)
The correct Answer is:A
To find the work done in stacking 'n' identical cubes, each of mass 'm' and edge 'L', we need to calculate the change in gravitational potential energy as the cubes are moved from their initial position to their final stacked position.
1. Understanding the Initial Configuration:
- Initially, all 'n' cubes are on the floor. The gravitational potential energy (U_i) of each cube at this position is zero since we can consider the floor level as our reference point (U = 0).
Hint: Remember that potential energy is measured relative to a reference point, and we can set the floor as zero potential energy.
2. Calculating the Final Configuration:
- When the cubes are stacked vertically, the center of mass of each cube will be at different heights. The height of the center of mass of the first cube (bottom) is L/2, the second cube is at 3L/2, the third at 5L/2, and so on, up to the nth cube.
3. Height of Each Cube's Center of Mass:
- The height of the center of mass for the ith cube can be expressed as:
hi=(i−12)Lfor i=1,2,…,n
4. Calculating the Total Final Potential Energy (U_f):
- The potential energy of each cube at height hi is given by U=mgh.
- Therefore, the total potential energy when all cubes are stacked is:
Uf=n∑i=1mghi=mgn∑i=1(i−12)L
- This can be simplified to:
Uf=mgLn∑i=1(i−12)=mgL(n∑i=1i−n2)
5. Using the Formula for the Sum of the First n Natural Numbers:
- The sum of the first n natural numbers is given by:
n∑i=1i=n(n+1)2
- Substituting this into our equation for Uf:
Uf=mgL(n(n+1)2−n2)=mgL(n22+n2−n2)=mgLn22
6. Calculating the Work Done (W):
- The work done in stacking the cubes is equal to the change in potential energy:
W=Uf−Ui=mgLn22−0=mgLn22
7. Final Expression for Work Done:
- Thus, the work done in stacking the cubes is:
W=n(n−1)2mgL
Final Answer:
The work to be done to stack 'n' identical cubes each of mass 'm' and edge 'L' is:
W=n(n−1)2mgL
- Initially, all 'n' cubes are on the floor. The gravitational potential energy (U_i) of each cube at this position is zero since we can consider the floor level as our reference point (U = 0).
- When the cubes are stacked vertically, the center of mass of each cube will be at different heights. The height of the center of mass of the first cube (bottom) is L/2, the second cube is at 3L/2, the third at 5L/2, and so on, up to the nth cube.
- The height of the center of mass for the ith cube can be expressed as:
hi=(i−12)Lfor i=1,2,…,n
- The potential energy of each cube at height hi is given by U=mgh.
- Therefore, the total potential energy when all cubes are stacked is:
Uf=n∑i=1mghi=mgn∑i=1(i−12)L
- This can be simplified to:
Uf=mgLn∑i=1(i−12)=mgL(n∑i=1i−n2)
- The sum of the first n natural numbers is given by:
n∑i=1i=n(n+1)2
- Substituting this into our equation for Uf:
Uf=mgL(n(n+1)2−n2)=mgL(n22+n2−n2)=mgLn22
- The work done in stacking the cubes is equal to the change in potential energy:
W=Uf−Ui=mgLn22−0=mgLn22
- Thus, the work done in stacking the cubes is:
W=n(n−1)2mgL
The work to be done to stack 'n' identical cubes each of mass 'm' and edge 'L' is:
W=n(n−1)2mgL
Topper's Solved these Questions
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level- III (C.W)
50 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - NCERT (Based Questions)
45 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level- I (C.W)
60 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
Identical cubes each of mass 'm' and side T' are on the horizontal surface.Then the minimum amount of work done to arrange them one on the other is
View SolutionIf n number of identical cubes, each of mass m and side a lying on level ground. Find the work done in piling them one above the other.
View Solution
Knowledge Check
A meter scale of mass 400gm is lying horizontally on the floor. If it is to be held vertically with one end touching the floor, the work to be done is
A6JB4JC40JD2J125 identical cubes are cut from a big cube and all the smaller cubes are arranged in a row to form a long cuboid . What is the percentage increase in the total surface area of the cuboid over the total surface area of the cube ?
A23423%B23513%C13423%Dnone of theseSix identical particles each of mass m are arranged at the corners of a regular hexagon of side length L. If the mass of one of the particle is doubled, the shift in the centre of mass is
ALB6L/7CL/7DL√3
Four identical spheres each of mass M and radius R are placed on the vertices of a square of edge L. Find the M.I. about an axis
(a) coinciding with the side of a square and
(b) coinciding with the diagonal of a square.
View SolutionTwelve identical wires each of resistance 6Ω are joined to from a skeleton cube. Find the resistance between the current of the same edge of the cube
View SolutionWhen a torch is pointed towards one of the vertical edges of a cube, you get a shadow of cube in the shape of
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
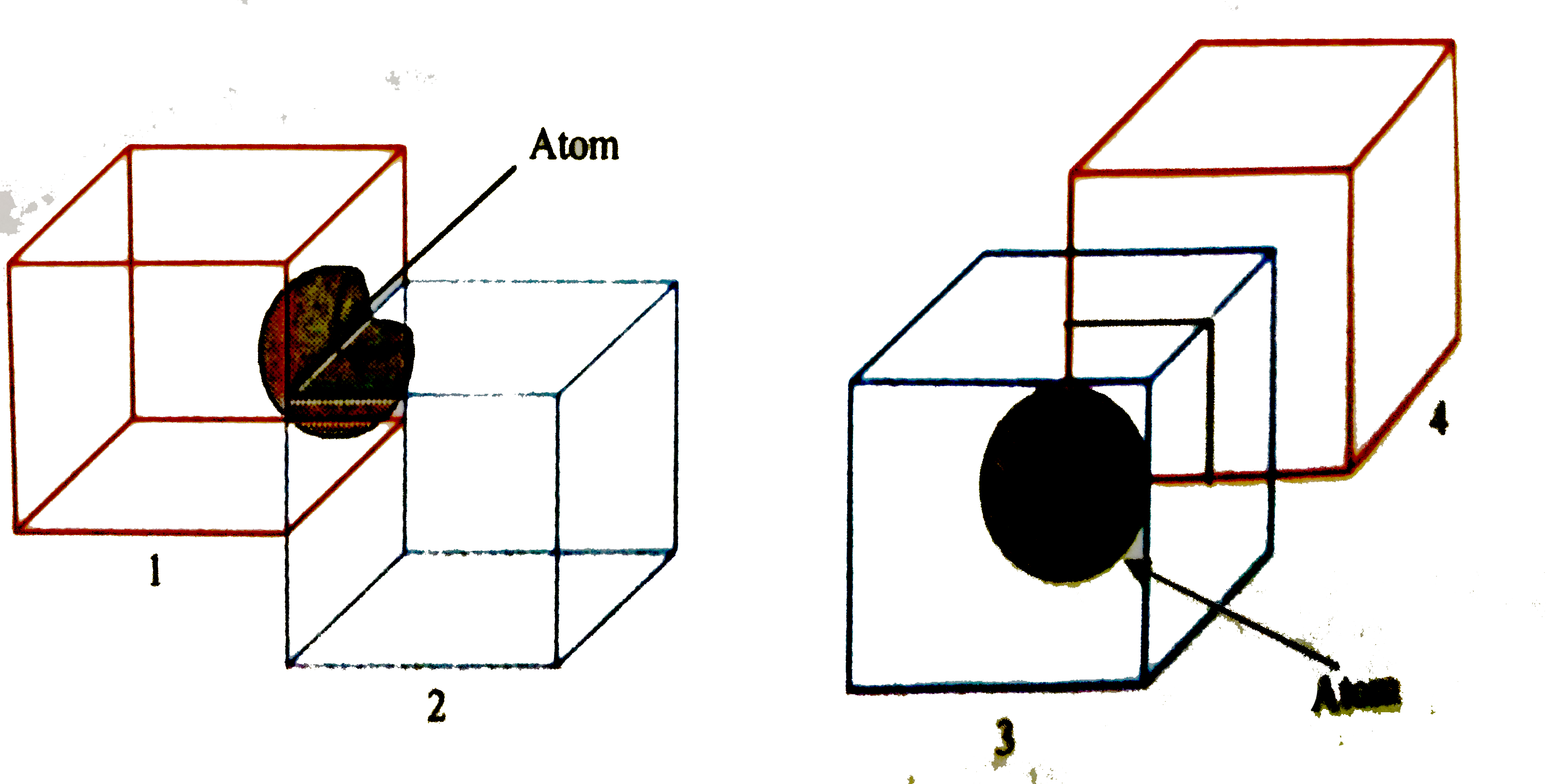
View SolutionFollowing frightening diagrams show identical cubes such that edge of cube 2 lies exactly in the middle of one of the faces of Cube 1 and Cube 4 has a corner at the body centre of the cube 3 . Find the contribution (in fraction) of the spheres shown to each of the cube 1 ,2 , 3 and 4 respectively is
View Solution
