When the road is dry and coefficient of friction is μ. the maximum speed of a cur in a circular path is 10m/sec, If the road becomes wet and μ1=μ/2. What is the maximum speed permitted
5m/sec
10m/sec
10√2m/sec
5√2m/sec
The correct Answer is:D
To solve the problem step by step, we need to analyze the forces acting on a car moving in a circular path and how they change when the coefficient of friction changes due to wet conditions.
1. Understanding the Forces:
When a car is moving in a circular path, the frictional force provides the necessary centripetal force to keep the car in motion. The maximum frictional force can be expressed as:
fmax=μ⋅N
where N is the normal force, which in this case is equal to the weight of the car mg.
2. Setting Up the Equation for Dry Conditions:
For the dry road, the maximum speed v of the car is given as 10m/s. The centripetal force required for circular motion can be expressed as:
fmax=mv2r
Setting the frictional force equal to the centripetal force, we have:
μmg=mv2r
Here, the mass m cancels out, leading to:
μg=v2r
3. Calculating for Wet Conditions:
When the road becomes wet, the coefficient of friction changes to μ′=μ2. We need to find the new maximum speed v′:
μ′mg=mv′2r
Again, canceling m gives:
μ2g=v′2r
4. Relating the Two Conditions:
From the dry condition, we have:
μg=102r(since v=10 m/s)
Substituting this into the wet condition:
μ2g=v′2r
This implies:
12(102r)=v′2r
Thus, we can simplify to:
1002=v′2
Therefore:
v′2=50
5. Finding the Maximum Speed:
Taking the square root gives:
v′=√50=5√2m/s
Final Answer:
The maximum speed permitted when the road is wet is 5√2m/s.
When a car is moving in a circular path, the frictional force provides the necessary centripetal force to keep the car in motion. The maximum frictional force can be expressed as:
fmax=μ⋅N
where N is the normal force, which in this case is equal to the weight of the car mg.
For the dry road, the maximum speed v of the car is given as 10m/s. The centripetal force required for circular motion can be expressed as:
fmax=mv2r
Setting the frictional force equal to the centripetal force, we have:
μmg=mv2r
Here, the mass m cancels out, leading to:
μg=v2r
When the road becomes wet, the coefficient of friction changes to μ′=μ2. We need to find the new maximum speed v′:
μ′mg=mv′2r
Again, canceling m gives:
μ2g=v′2r
From the dry condition, we have:
μg=102r(since v=10 m/s)
Substituting this into the wet condition:
μ2g=v′2r
This implies:
12(102r)=v′2r
Thus, we can simplify to:
1002=v′2
Therefore:
v′2=50
Taking the square root gives:
v′=√50=5√2m/s
The maximum speed permitted when the road is wet is 5√2m/s.
Similar Questions
When the road is dry and coefficient of friciton is μ, the maximum speed of a car in a circular path is 10ms−1. If the road becomes wet and coefficient of friction becomes μ4, what is the maximum speed permited ?
View SolutionIn the figure shown if coefficient of friction is μ, then m2 will start moving upwards if
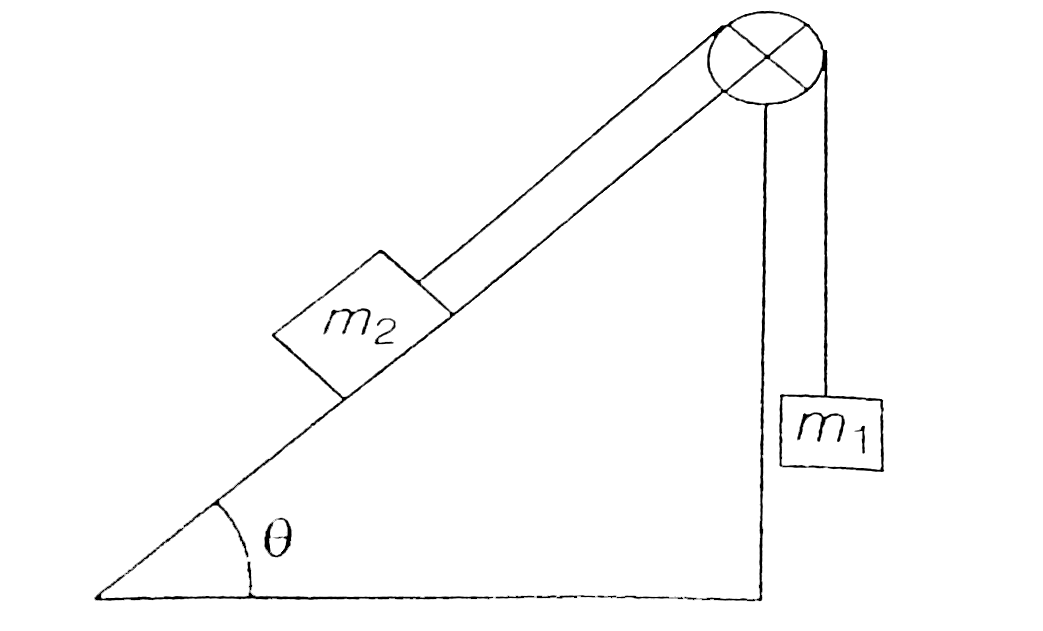
View Solution
Knowledge Check
A circular racetrack of radius 300 m is banked at an angle of 15∘ If the coefficient of friction between the wheels of a race car and the road is 0.2 what is the (a) optimum speed of the race car to avoid wear and tear on its tyres , and (b) maximum permissible speed to aviod slipping ?
A10√3ms−1B9√10ms−1C√10ms−1D2√10ms−1A block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)
A circular racetrack of radius 300 m is banked at an angle of 15∘ If the coefficient of friction between the wheels of a race car and the road is 0.2 what is the (a) optimum speed of the race car to avoid wear and tear on its tyres , and (b) maximum permissible speed to aviod slipping ?
View SolutionA circular racetrack of radius 300 m is banked at an angle of 15∘ The coefficient of friction between the wheels of a race car and the road is 0.2. The optimum speed of the race car to avoid wear and tear on its tyres is
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionTwo particles of mass m each are kept on a horizontal circular platfrom on two mutually perpendicular radii at equal distance r from the center of the table. The particles are connected with a string, which is just taught when the platfrom is not rotating. The coefficient of static friction between the platfrom and block is μ (now if angular speed of platfrom m is slowly increased). Find the maximum angular speed (ω) of platfrom about it center so that the blocks remain stationery relative to platform. (If μ=1√2, r=2.5m and g=10m/s2)
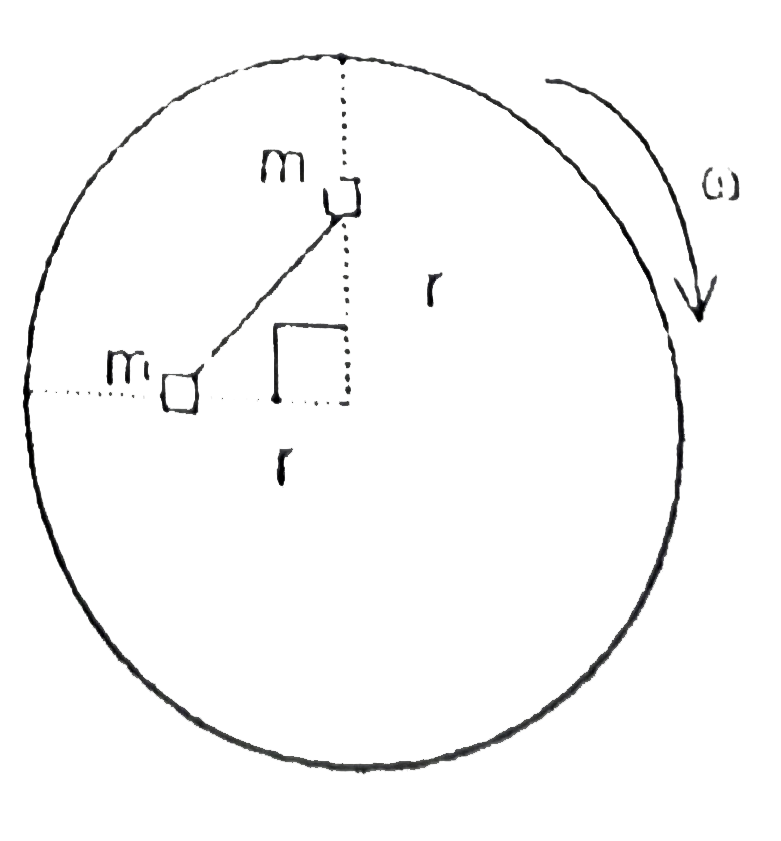
View SolutionA block is projected with a speed v0 such that it strikes the point of projection after describing the path as shown by the dotted line. If friction exists for the parth of length d and the vertical circular path is smooth, assuming μ=coefficient of friction,
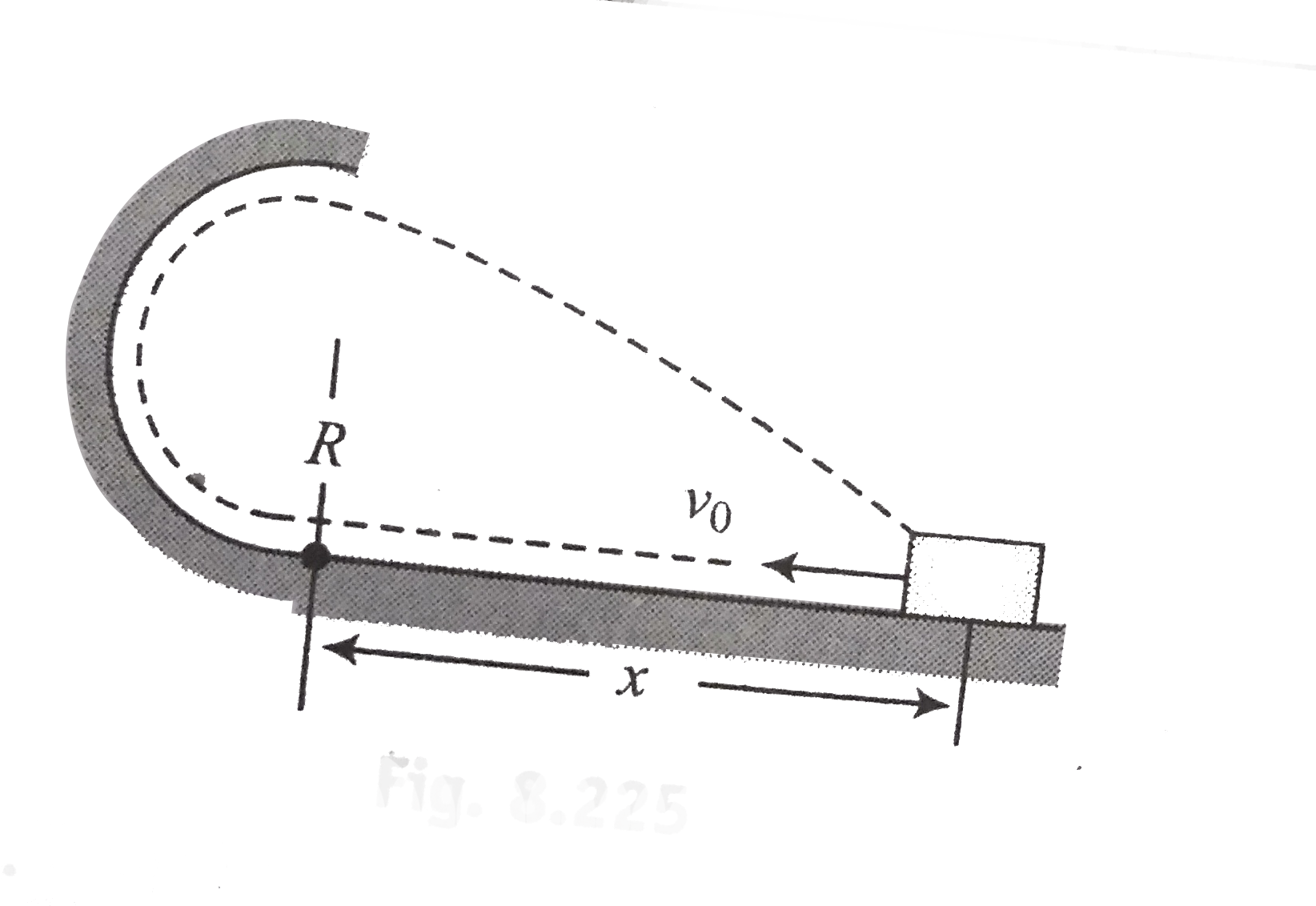
a. Find v0.
b. What is the minimum value of v0?
View Solution
