Two particles of mass m each are kept on a horizontal circular platfrom on two mutually perpendicular radii at equal distance r from the center of the table. The particles are connected with a string, which is just taught when the platfrom is not rotating. The coefficient of static friction between the platfrom and block is μ (now if angular speed of platfrom m is slowly increased). Find the maximum angular speed (ω) of platfrom about it center so that the blocks remain stationery relative to platform. (If μ=1√2, r=2.5m and g=10m/s2)
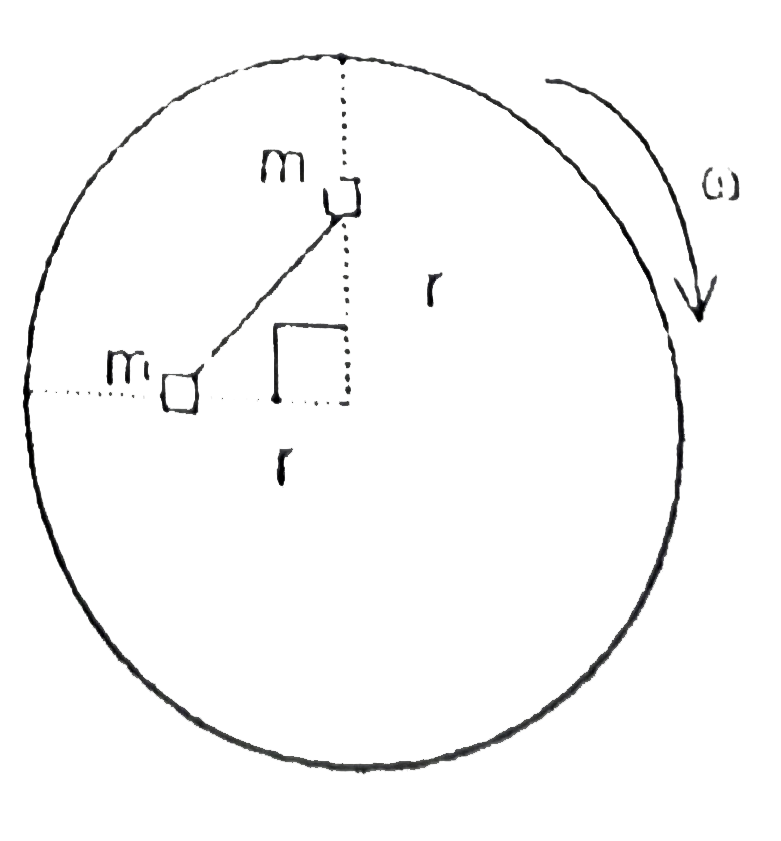
For small values of ω friction will be directed radially inwards as the tension in the spring is zero. The string will develop tension only if the centinfugal force FC exceeds the limiting friction fc. i.e. when
mω2r>μmg (fc=μmg)
or ω=√μgr
in this case direction of friction will be as shown in the figure.
For equilibrium
Fc=Tcos45∘+fccosθ
And Tsin45∘=fcsinθ
Eliminiating T, we get
Fc=fc(sinθ+cosθ)
i.e. mω2r=μmg[√2sin(θ+45∘)]
or ω2=√2μgrsin(θ+45∘)
maximum value of sin(θ+45∘) is 1
∴ Maximum value of ω=√√2μgr=2

Similar Questions
Two particles of mass M=3kg each are kept on a horizontal circular platform on two mutually perpendicular radii at equal distance R=1m from the centre of the table. The particles are connected with a string,which is just taught when the platform is not rotating.Coefficient of friction between the platform and block is μ=0.4.Then the maximum angular speed (ω in radsec) of platform about its centre so that the blocks remain stationary relative to platform is (take g=10.ms2 )
View SolutionA block on table shown in figure is just on the wedge of slipping. Find the coefficient of static friction between the block and table top.

View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mg
Coefficient of kinetic friction and coefficient of static friction between two blocks is μk and μs respectively. In general
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionA block is on horizontal slab which is moving horizontally and excuting S.H.M. The coefficient of static frication between block and slab is μ. If block is not separated from slab then determine range of angular frequency of oscillation.
View SolutionA block of mass M is in contact with a cart of mass M. The coefficient of static friction between block and cart is μ . To prevent the block from sliding on cart, acceleration a should be
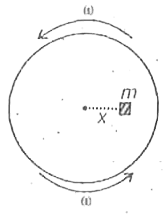
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View Solution
