An X-ray beam (λ=70.9pm) was scattered by a crystalline solid. The angle (2θ) of the diffraction for a second order reflection is 14.660. Calculate the distance between parallel planes of atoms of the crystalline solid.
To solve the problem of calculating the distance between parallel planes of atoms in a crystalline solid using Bragg's law, we can follow these steps:
Step 1: Understand Bragg's Law
Bragg's law states that:
nλ=2dsinθ
where:
- n is the order of reflection,
- λ is the wavelength of the X-ray,
- d is the distance between the planes of atoms,
- θ is the angle of reflection.
Step 2: Identify Given Values
From the problem, we have:
- Wavelength λ=70.9pm=70.9×10−12m
- The angle 2θ=14.66∘ implies that θ=14.662=7.33∘
- The order of reflection n=2
Step 3: Calculate sinθ
Convert θ to radians if necessary, but since we can use degrees directly in most calculators:
sin(7.33∘)
Using a calculator:
sin(7.33∘)≈0.127
Step 4: Rearrange Bragg's Law to Solve for d
Rearranging Bragg's law gives:
d=nλ2sinθ
Step 5: Substitute the Values
Substituting the known values into the equation:
d=2×(70.9×10−12m)2×0.127
Step 6: Simplify the Equation
The 2s cancel out:
d=70.9×10−120.127
Step 7: Calculate d
Now performing the calculation:
d≈70.9×10−120.127≈5.58×10−10m
Step 8: Convert to Picometers
To express d in picometers:
d≈558pm
Final Answer
The distance between parallel planes of atoms in the crystalline solid is approximately 558 pm.
---
Bragg's law states that:
nλ=2dsinθ
where:
- n is the order of reflection,
- λ is the wavelength of the X-ray,
- d is the distance between the planes of atoms,
- θ is the angle of reflection.
From the problem, we have:
- Wavelength λ=70.9pm=70.9×10−12m
- The angle 2θ=14.66∘ implies that θ=14.662=7.33∘
- The order of reflection n=2
Convert θ to radians if necessary, but since we can use degrees directly in most calculators:
sin(7.33∘)
sin(7.33∘)≈0.127
Rearranging Bragg's law gives:
d=nλ2sinθ
Substituting the known values into the equation:
d=2×(70.9×10−12m)2×0.127
The 2s cancel out:
d=70.9×10−120.127
Now performing the calculation:
d≈70.9×10−120.127≈5.58×10−10m
To express d in picometers:
d≈558pm
The distance between parallel planes of atoms in the crystalline solid is approximately 558 pm.
Similar Questions
A sample of a crystalline solid scatters a beam of X-rays of wavelength 70.93 pm at an angle 2θ of 14.66∘. If this is a second-order reflection (n=2), calculate the distance between the parallel planers of atoms from which the scattered beam appears to have been reflected.
View SolutionThe second order Bragg diffraction of X-rays with λ=1.0Å from a set of parallel planes in a metal occurs at an angle 60∘. The distance between the scattering planes in the crystals is
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
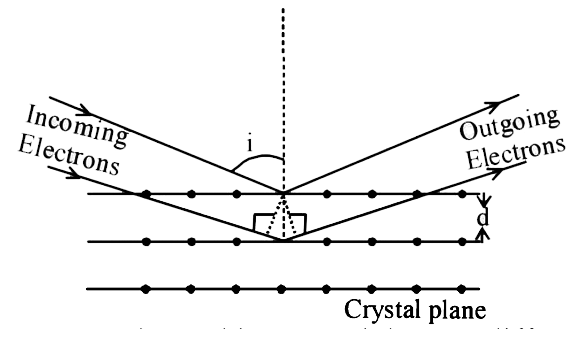
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
View SolutionVertices of a parallelogram taken in order are A, ( 2,-1,4) , B (1,0,-1) , C ( 1,2,3) and D (x,y,z) The distance between the parallel lines AB and CD is
View SolutionA beam of light of wavelength 600 nm from a distant source falls on a single slit 1.0 mm wide and the resulting diffraction pattern is observed on a screen 2 m away What is the distance between the second bright fringe on either side of the central bright fringe ?
View SolutionThe interplanar distance in a crystal used for X - ray diffraction is 2A0. The angle of incidence for first order diffraction is 9°, what is the wave length of X - rays?
View SolutionTwo plane mirrors are inclined at 70∘. A ray incident on one mirror at incidence angle θ after reflection falls on the second mirror and is reflected from there parallel to the first mirror, The value of θ is
View SolutionAssertion: Crystalline solids can cause X-rays to diffract.
Reason: Interatomic distance in crystalline solids is of the order of 0.1nm.
View SolutionCalculate the angle at which first order reflection will occur in an X-ray spectrometer when X-rays of wavelength 1.54Å are diffracted by the atoms of a crystal given that interplanar distance is 0.04Å.
View SolutionThe distance between planes of ions parallel of the unit cell of sodium chloride is 282 pm. The smallest angle of reflection observed in the X-ray diffraction pattern is 5.97∘ . Calculate the wavelength of the incident radiation.
View Solution
