The interplanar distance in a crystal used for X - ray diffraction is 2A0. The angle of incidence for first order diffraction is 9°, what is the wave length of X - rays?
To solve the problem, we will use Bragg's law, which is given by the equation:
nλ=2dsinθ
Where:
- n is the order of diffraction (given as 1 for first order),
- λ is the wavelength of the X-rays,
- d is the interplanar distance,
- θ is the angle of incidence.
1. Identify the given values:
- Interplanar distance, d = 2 \, \text{Å} = 2 \times 10^{-10} \, \text{m}
- Angle of incidence, θ=9∘
- Order of diffraction, n=1
2. Convert the angle from degrees to radians (if necessary):
- However, for this calculation, we can use the sine function directly in degrees.
3. Use Bragg's Law:
- Substitute the known values into Bragg's equation:
nλ=2dsinθ
1λ=2×(2Å)×sin(9∘)
4. Calculate sin(9∘):
- Using a calculator, we find:
sin(9∘)≈0.1564
5. Substitute sin(9∘) back into the equation:
λ=2×2Å×0.1564
λ=4×0.1564Å
6. Calculate λ:
λ≈0.6256Å
7. Final Result:
- Rounding off, we can state:
λ≈0.63Å
Final Answer:
The wavelength of the X-rays is approximately 0.63Å.
- n is the order of diffraction (given as 1 for first order),
- λ is the wavelength of the X-rays,
- d is the interplanar distance,
- θ is the angle of incidence.
- Interplanar distance, d = 2 \, \text{Å} = 2 \times 10^{-10} \, \text{m}
- Angle of incidence, θ=9∘
- Order of diffraction, n=1
- However, for this calculation, we can use the sine function directly in degrees.
- Substitute the known values into Bragg's equation:
nλ=2dsinθ
1λ=2×(2Å)×sin(9∘)
- Using a calculator, we find:
sin(9∘)≈0.1564
λ=2×2Å×0.1564
λ=4×0.1564Å
λ≈0.6256Å
- Rounding off, we can state:
λ≈0.63Å
The wavelength of the X-rays is approximately 0.63Å.
Similar Questions
What is the angle of incidence when incident Ray is normal to the interface between the 2 media?
View SolutionThe first − order diffraction os X− rays from a certain set of crystal planes occurs an angle of 11.8∘ from the planes. If the planes are 0.281nm apart, what is the wavelength of X− rays?
View SolutionA ray of light is normally incident on one face of an equilateral glass prism. Answer the following :
(a) What is the angle of incidence on the first face of the prism?
(b) What is the angle of refraction from the first face of the prism ?
(c) What will be the angle of incidence at the second face of the prism ?
(d) Will the light ray suffer minimum deviation by the prism ?
View SolutionCalculate λ of X-rays which give a diffraction angle 2θ=16.8∘ for crystal, if the interplanar distance in the crystal is 0.2nm and that only for the first-order diffraction is observed. Given sin8.40∘=0.146.
View SolutionWhat will be the angle of diffracting for the first minimum due to Fraunhofer diffraction with sources of light of wavelength 550nm and slit of width 0.55mm?
View SolutionWilkin's X-ray diffraction showed the diameter of the DNA helix as :
View SolutionThe distance between planes of ions parallel of the unit cell of sodium chloride is 282 pm. The smallest angle of reflection observed in the X-ray diffraction pattern is 5.97∘ . Calculate the wavelength of the incident radiation.
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
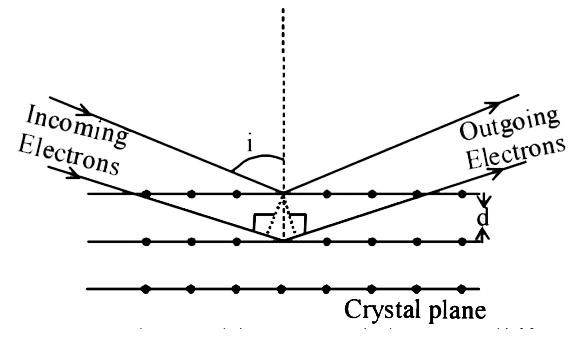
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
View SolutionA ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
View SolutionAt what angle for the first - order diffraction, spacing between two planes respectively is λandλ2?
View Solution
