The distance between planes of ions parallel of the unit cell of sodium chloride is 282 pm. The smallest angle of reflection observed in the X-ray diffraction pattern is 5.97∘ . Calculate the wavelength of the incident radiation.
To solve the problem, we will use Bragg's Law, which is given by the equation:
nλ=2Dsinθ
Where:
- n = order of reflection (for the smallest angle, we take n=1)
- λ = wavelength of the incident radiation
- D = distance between the planes of ions (given as 282 pm)
- θ = angle of reflection (given as 5.97°)
Step 1: Identify the known values.
- Distance between planes of ions, D=282 pm = 282×10−12 m
- Angle of reflection, θ=5.97∘
- Order of reflection, n=1
Step 2: Convert the angle from degrees to radians (if necessary).
- In this case, we can directly use the sine function in degrees, so we do not need to convert it.
Step 3: Calculate sinθ.
- Use a calculator to find sin(5.97∘).
sin(5.97∘)≈0.103
Step 4: Substitute the values into Bragg's Law.
- Using n=1, D=282×10−12 m, and sin(5.97∘):
1⋅λ=2⋅(282×10−12)⋅0.103
Step 5: Calculate λ.
- First, calculate 2Dsinθ:
2Dsinθ=2⋅282×10−12⋅0.103≈58.6×10−12 m
Thus,
λ≈58.6 pm
Step 6: Convert the wavelength to meters if required.
- To convert picometers to meters:
λ=58.6 pm=58.6×10−12 m=5.86×10−11 m
Final Answer:
The wavelength of the incident radiation is 58.6 pm or 5.86×10−11 m.
- n = order of reflection (for the smallest angle, we take n=1)
- λ = wavelength of the incident radiation
- D = distance between the planes of ions (given as 282 pm)
- θ = angle of reflection (given as 5.97°)
- Distance between planes of ions, D=282 pm = 282×10−12 m
- Angle of reflection, θ=5.97∘
- Order of reflection, n=1
- In this case, we can directly use the sine function in degrees, so we do not need to convert it.
- Use a calculator to find sin(5.97∘).
sin(5.97∘)≈0.103
- Using n=1, D=282×10−12 m, and sin(5.97∘):
- First, calculate 2Dsinθ:
- To convert picometers to meters:
The wavelength of the incident radiation is 58.6 pm or 5.86×10−11 m.
Similar Questions
In the distance between Na+ and CI− ions in sodium
chloride crystal is y pm , the length of the edge of the unit cell is
View SolutionEdge length of unit cell of KCI is 629 pm and density is 1.989 g per cm3. Calculate Avogadro's number based on this X-ray diffraction data.
View Solution
The distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror forms image at the optical centre of the lens. Focal length of lens will be
View SolutionThe distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror form image at the optical centre of the lens. Focal length of lens will be

View SolutionLight of wavelength 6000Å is incident on a thin glass plate of refractive index 1.5 such that angle of refraction into the plate is 60∘. Calculate the smallest thickness of plate which will make it appear dark by reflection.
View SolutionA double - slit apparatus is immersed in a liquid of refractive index 1.33 it has slit separation of 1mm and distance between the plane of slits and screen 1.33 m the slits are illuminated by a parallel beam of light whose wavelength in air is 800 nm.
(i) Calculate the fringe width.
(ii) One of the slits of apparatus is covered by a thin glass sheet of refractive index 1.53 Find the smallest thickness of the sheet to bring the adjacent minima on the axis.
View SolutionThe distance between the first and fifth minima of a single slit diffraction patterns is 0.40 mm with screen 50 cm away from the slit, using light of wavelength 550 . (a) Find the slit width (b) Calculate the angle of the first diffraction minimum
View SolutionIn YDSE using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.5 and thickness 2 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the plane of slits and the screen is doubled. It is found that the distance between successive maxima (or minima) now is the same as the observed fringe shift upon the introduction of the mica sheet. Calculate the wavelength of the light.
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
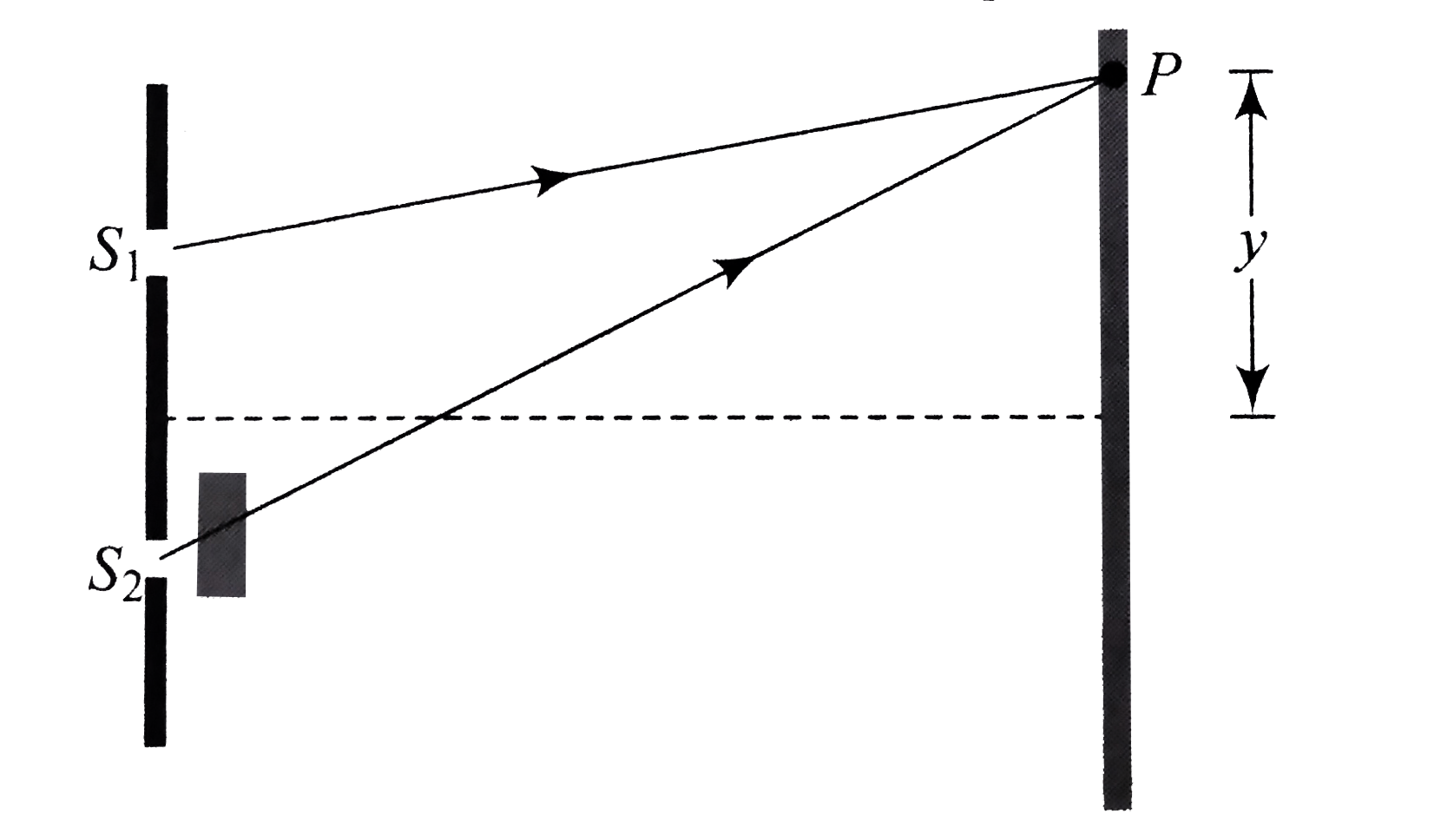
The value of η is
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
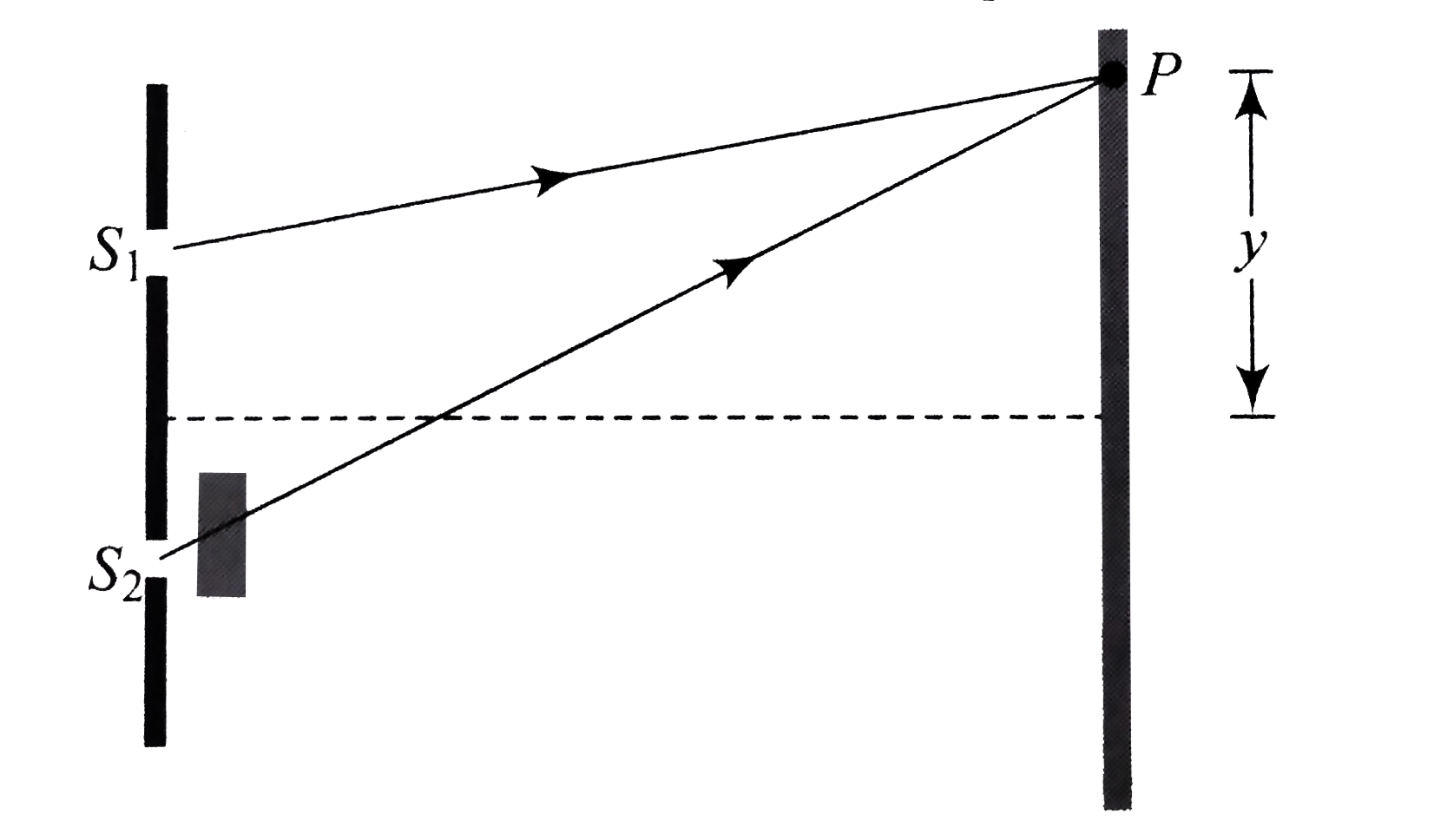
Intensity at point P is
View Solution

