The variation of momentum with time of one of the body in a two body collision is shown. At what point the instantaneous force is maximum.
To determine at which point the instantaneous force is maximum in the given momentum-time graph for one of the bodies in a two-body collision, we can follow these steps:
Step 1: Understand the relationship between force and momentum
According to Newton's second law of motion, the force acting on an object is equal to the rate of change of momentum with respect to time. Mathematically, this is expressed as:
F=dpdt
where F is the force, p is the momentum, and t is the time.
Step 2: Analyze the momentum-time graph
The graph plots momentum (on the y-axis) against time (on the x-axis). The slope of the momentum-time graph at any point gives the instantaneous force at that point. Therefore, we need to determine the slope of the graph at points P, Q, R, and S.
Step 3: Calculate the slope at each point
- Point P: Determine the slope of the tangent line at point P.
- Point Q: Determine the slope of the tangent line at point Q.
- Point R: Determine the slope of the tangent line at point R.
- Point S: Determine the slope of the tangent line at point S.
Step 4: Compare the slopes
After calculating the slopes at each of the points (P, Q, R, S), compare these values. The point with the steepest slope corresponds to the maximum instantaneous force.
Step 5: Identify the point with maximum force
From the comparison, identify which point has the maximum slope. This point is where the instantaneous force is maximum.
Conclusion
Based on the analysis, the instantaneous force is maximum at point R because the slope of the momentum-time graph is steepest at this point.
---
According to Newton's second law of motion, the force acting on an object is equal to the rate of change of momentum with respect to time. Mathematically, this is expressed as:
F=dpdt
where F is the force, p is the momentum, and t is the time.
The graph plots momentum (on the y-axis) against time (on the x-axis). The slope of the momentum-time graph at any point gives the instantaneous force at that point. Therefore, we need to determine the slope of the graph at points P, Q, R, and S.
- Point P: Determine the slope of the tangent line at point P.
- Point Q: Determine the slope of the tangent line at point Q.
- Point R: Determine the slope of the tangent line at point R.
- Point S: Determine the slope of the tangent line at point S.
After calculating the slopes at each of the points (P, Q, R, S), compare these values. The point with the steepest slope corresponds to the maximum instantaneous force.
From the comparison, identify which point has the maximum slope. This point is where the instantaneous force is maximum.
Based on the analysis, the instantaneous force is maximum at point R because the slope of the momentum-time graph is steepest at this point.
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:Application
Explore 6 Videos
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:EXERCISE - I
Explore 157 Videos
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:QUESTIONS FOR DESCRIPTIVE ANSWER
Explore 5 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 10 Videos
- LOGIC GATESBook:AAKASH SERIESChapter:LOGIC GATESExercise:Exercise (Very Short Answer)
Explore 10 Videos
Similar Questions
What is the effect of force on a rigid body ?
View SolutionVelocity-time graph for the motion of a certain body is shown in Fig. Explain the nature of this motion. Find the initial velocity and acceleration and write the equation for the variation of displacement with time. What happens to the moving body at point B? How does the body move after this moment ?
View Solution
Knowledge Check
The gravitational force between two bodies is :
Aalways repulsiveBalways attractiveCattractive only at large distancesDrepulsive only at large distances.
The variation of angular position θ, of a point on a rotating rigid body, with time t is shown in Fig. Is the body rotating clock wise or anti-clockwise ?
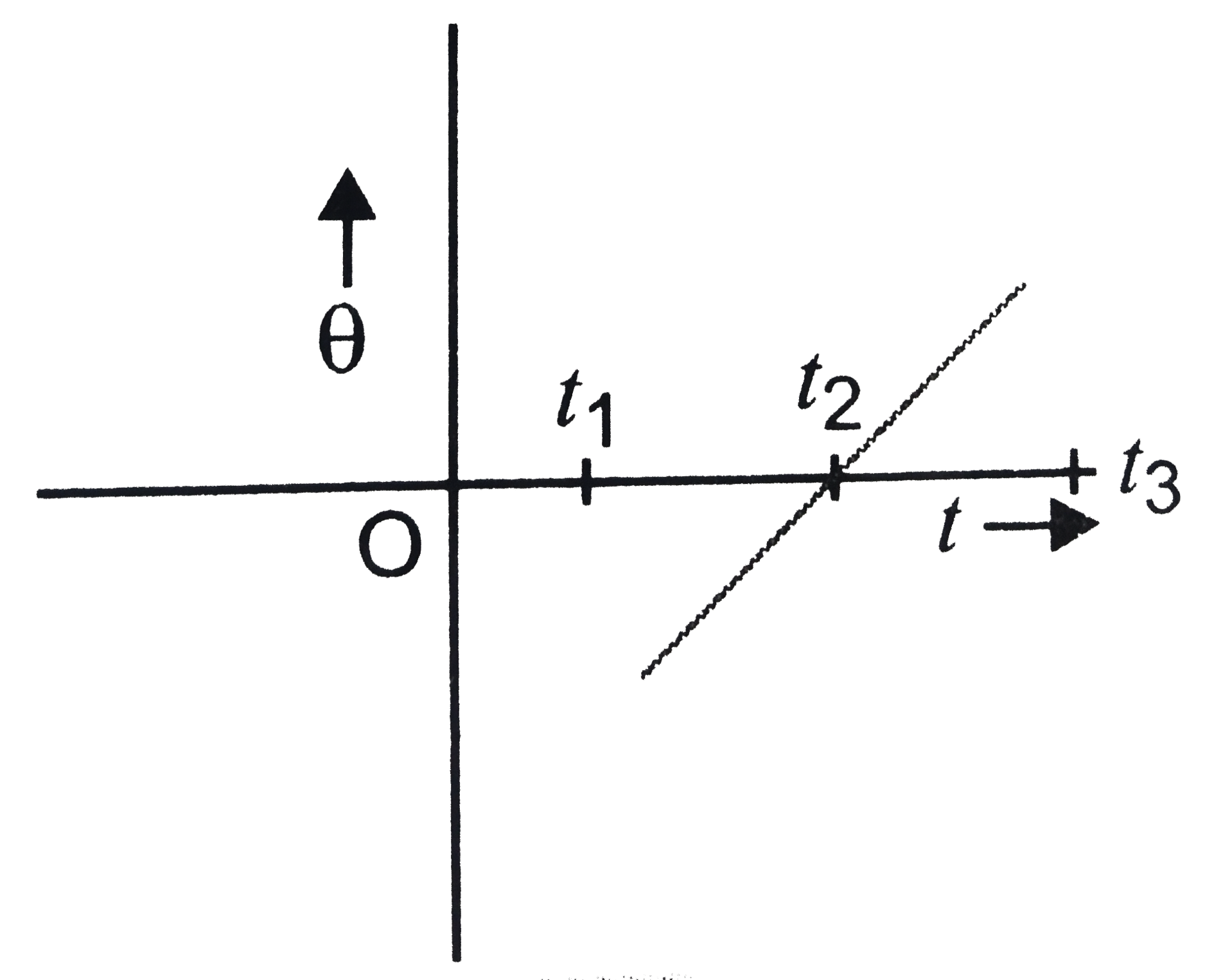
View SolutionThe variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
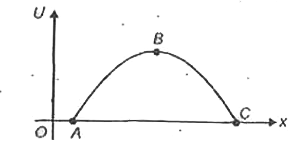
The body is in equilibrium state at
View SolutionThe velocity time graph of a body is shown in fig. it indicates that :

View SolutionIf the distance between the two bodies is increased to two times, then by how many times the mass of one of the bodies to be changed to maintain the same gravitational force ?
View SolutionOn applying force to the centre of mass of a body one of the following is present in the body?
View Solutionthe variaton of angular postion θ of a point on a rotating rigid body with time t is shown in figure Is the body rotating clokwise or anti- clokwise ?
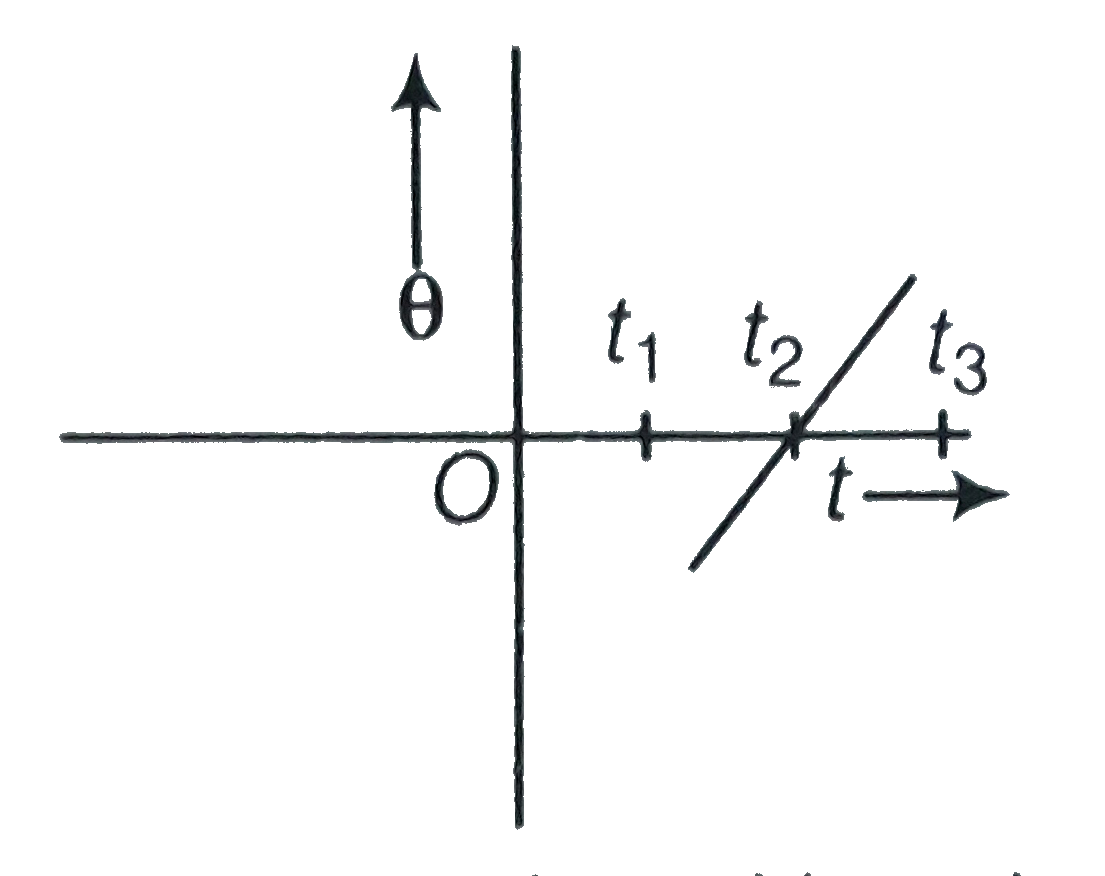
View SolutionSTATEMENT-l : In an elastic collision between two bodies, the relative speed of the bodies after collision is equal to the relative speed before the collision.
STATEMENT-2 : In an elastic collision, the linear momentum of the system is conserved.
View Solution

