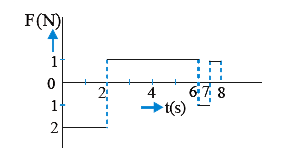
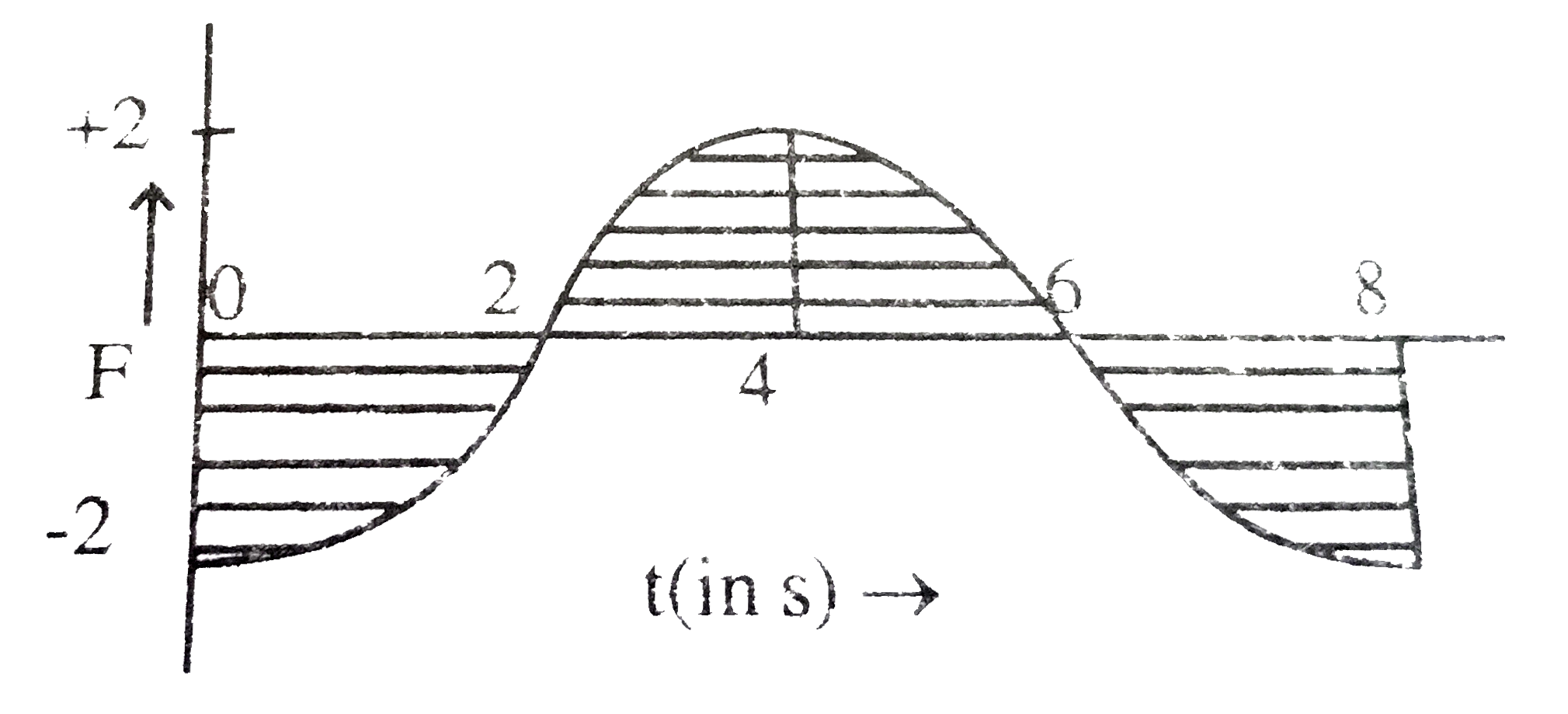Velocity-time graph for the motion of a certain body is shown in Fig. Explain the nature of this motion. Find the initial velocity and acceleration and write the equation for the variation of displacement with time. What happens to the moving body at point B? How does the body move after this moment ?
To solve the problem regarding the velocity-time graph and the motion of the body, we will follow these steps:
Step 1: Analyze the Velocity-Time Graph
The velocity-time graph typically shows how the velocity of an object changes over time. The slope of the graph indicates acceleration, while the area under the graph represents displacement.
Step 2: Determine Initial Velocity
From the graph, we can find the initial velocity (v₀) at time t = 0. This is the value of the velocity at the start of the motion.
Solution:
- If the graph starts at a certain point on the velocity axis, that value is the initial velocity.
- For example, if the graph starts at 10 m/s, then the initial velocity v₀ = 10 m/s.
Step 3: Calculate Acceleration
The acceleration (a) can be determined from the slope of the velocity-time graph. The formula for acceleration is:
a=ΔvΔt
where Δv is the change in velocity and Δt is the change in time.
Solution:
- If the graph shows that the velocity increases from 10 m/s to 20 m/s over a time interval of 5 seconds, then:
a=20−105=105=2m/s2
Step 4: Write the Equation for Displacement
The displacement (s) can be found using the kinematic equation:
s = v₀t + \frac{1}{2}at^2
Solution:
- If v₀ = 10 m/s, a = 2 m/s², and t = 5 s, then:
s=10(5)+12(2)(52)
s=50+12(2)(25)
s=50+25=75m
Step 5: Analyze Motion at Point B
At point B, we need to determine what happens to the body. This could be a point where the body reaches maximum velocity, changes direction, or comes to rest.
Solution:
- If the graph indicates that the velocity at point B is 0 m/s, the body has come to rest. If it is at maximum velocity, it will continue moving in the same direction.
Step 6: Describe Motion After Point B
After point B, the motion of the body will depend on the nature of the graph. If the velocity decreases, the body may start decelerating or moving in the opposite direction.
Solution:
- If the velocity starts decreasing after point B, the body is decelerating. If it becomes negative, the body is moving in the opposite direction.
Summary of Solutions
- Initial Velocity (v₀) = 10 m/s (example)
- Acceleration (a) = 2 m/s² (example)
- Displacement (s) = 75 m (example)
- At point B, the body may come to rest or reach maximum velocity.
- After point B, the body may decelerate or change direction.
The velocity-time graph typically shows how the velocity of an object changes over time. The slope of the graph indicates acceleration, while the area under the graph represents displacement.
From the graph, we can find the initial velocity (v₀) at time t = 0. This is the value of the velocity at the start of the motion.
- If the graph starts at a certain point on the velocity axis, that value is the initial velocity.
- For example, if the graph starts at 10 m/s, then the initial velocity v₀ = 10 m/s.
The acceleration (a) can be determined from the slope of the velocity-time graph. The formula for acceleration is:
a=ΔvΔt
where Δv is the change in velocity and Δt is the change in time.
- If the graph shows that the velocity increases from 10 m/s to 20 m/s over a time interval of 5 seconds, then:
a=20−105=105=2m/s2
The displacement (s) can be found using the kinematic equation:
s = v₀t + \frac{1}{2}at^2
- If v₀ = 10 m/s, a = 2 m/s², and t = 5 s, then:
s=10(5)+12(2)(52)
s=50+12(2)(25)
s=50+25=75m
At point B, we need to determine what happens to the body. This could be a point where the body reaches maximum velocity, changes direction, or comes to rest.
- If the graph indicates that the velocity at point B is 0 m/s, the body has come to rest. If it is at maximum velocity, it will continue moving in the same direction.
After point B, the motion of the body will depend on the nature of the graph. If the velocity decreases, the body may start decelerating or moving in the opposite direction.
- If the velocity starts decreasing after point B, the body is decelerating. If it becomes negative, the body is moving in the opposite direction.
- Initial Velocity (v₀) = 10 m/s (example)
- Acceleration (a) = 2 m/s² (example)
- Displacement (s) = 75 m (example)
- At point B, the body may come to rest or reach maximum velocity.
- After point B, the body may decelerate or change direction.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)
22 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)
29 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
Knowledge Check
The velocity time graph of a body is shown in fig. 3.3. it implies that at point B
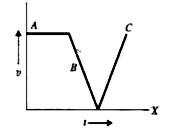 Athe force is zeroBthere is a force towards motionCthere is force which oppose motionDnone of the above
Athe force is zeroBthere is a force towards motionCthere is force which oppose motionDnone of the above
Velocity versus time graph of a body is shown in figure. It explains that

View SolutionThe velocity time graph of a body is shown in fig. it indicates that :

View SolutionThe diagram in Fig. shows the displacement time graph of a vibrating body.
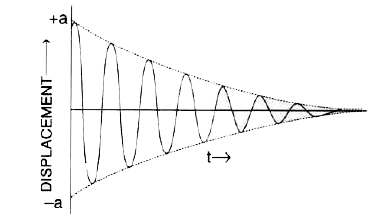
What happens to the vibrations of the body after some time?
View SolutionThe velocity-time graph of a body is shown in .
The displacement of the body in 8s is.
 .
.
View SolutionVelocity -time graph for a body of mass 10 kg is shown in figure. Work -done on the body in first two seconds of the motion is :
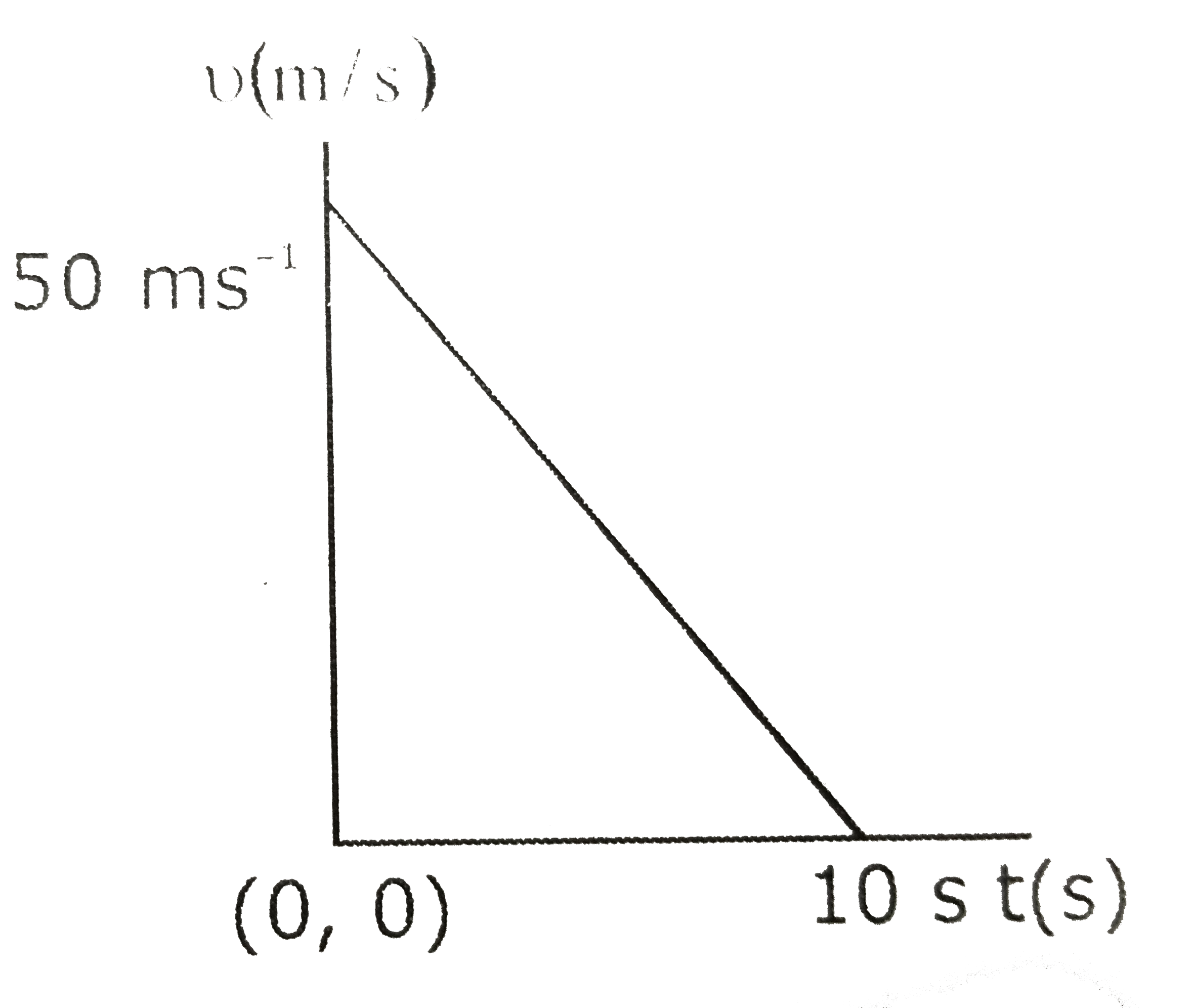
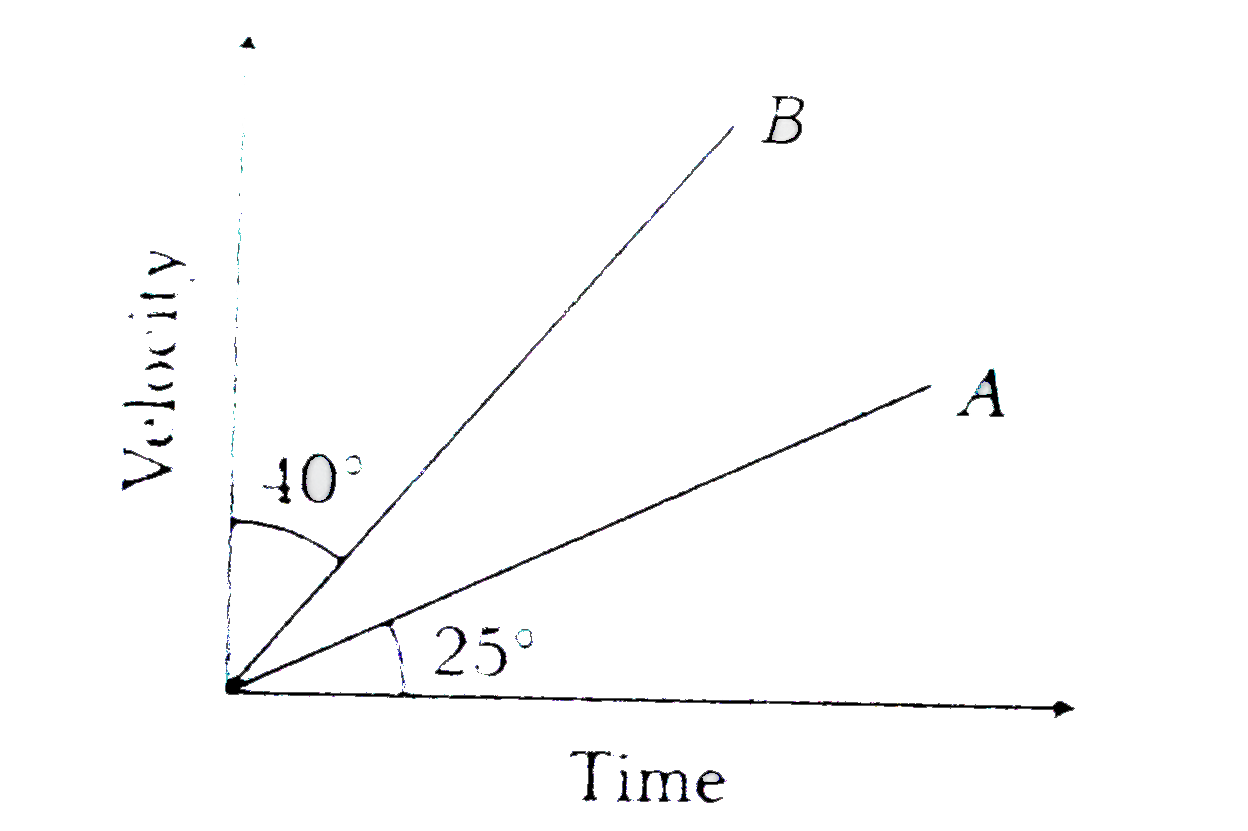
View SolutionThe velocity - time graph for two bodies A and B are shown in figure. Then, the acceleration of A and B are in the ratio
View SolutionThe diagram in Fig. shows the displacement time graph of a vibrating body.

What happens to the vibrations of the body after some time?
View Solution