A horizontal converyor belt moves with a constant velocity V. A small block is projected with a velocity of 6 mis on it in a direction opposite to the direction of motion of the belt. The block comes to rest relative to the belt in a time 4s. μ=0.3g,g=10m/s2
Find V
To solve the problem, let's break it down step by step:
Step 1: Understand the scenario
A block is projected on a conveyor belt moving with a constant velocity V. The block is initially moving in the opposite direction with a velocity of 6m/s and comes to rest relative to the belt in 4s.
Step 2: Identify the forces acting on the block
The forces acting on the block include:
- The gravitational force mg acting downwards.
- The normal force N acting upwards.
- The frictional force fr acting opposite to the direction of the block's motion.
Given that the coefficient of friction μ=0.3 and g=10m/s2, we can calculate the frictional force:
fr=μ⋅N=μ⋅mg
Step 3: Calculate the frictional force
Since N=mg, we have:
fr=μ⋅mg=0.3⋅m⋅10=3mN
Step 4: Determine the acceleration of the block
Using Newton's second law, the net force acting on the block is equal to the mass times its acceleration:
fr=m⋅a
Substituting for fr:
3m=m⋅a
Dividing both sides by m (assuming m≠0):
a=3m/s2
Step 5: Use kinematics to find the final velocity of the block
The block comes to rest relative to the belt after 4s. Using the kinematic equation:
v=u+at
where:
- u=6m/s (initial velocity of the block)
- a=−3m/s2 (deceleration due to friction)
- t=4s
Substituting the values:
v=6+(−3)⋅4=6−12=−6m/s
This means the block has a velocity of −6m/s relative to the ground after 4s.
Step 6: Relate the block's final velocity to the belt's velocity
At the moment the block comes to rest relative to the belt, its velocity relative to the ground is equal to the velocity of the belt V:
V=−6m/s
Since the block is moving in the opposite direction to the belt, we take the absolute value:
V=6m/s
Conclusion
The velocity of the conveyor belt V is 6m/s.
---
A block is projected on a conveyor belt moving with a constant velocity V. The block is initially moving in the opposite direction with a velocity of 6m/s and comes to rest relative to the belt in 4s.
The forces acting on the block include:
- The gravitational force mg acting downwards.
- The normal force N acting upwards.
- The frictional force fr acting opposite to the direction of the block's motion.
fr=μ⋅N=μ⋅mg
Since N=mg, we have:
fr=μ⋅mg=0.3⋅m⋅10=3mN
Using Newton's second law, the net force acting on the block is equal to the mass times its acceleration:
fr=m⋅a
Substituting for fr:
3m=m⋅a
Dividing both sides by m (assuming m≠0):
a=3m/s2
The block comes to rest relative to the belt after 4s. Using the kinematic equation:
v=u+at
where:
- u=6m/s (initial velocity of the block)
- a=−3m/s2 (deceleration due to friction)
- t=4s
v=6+(−3)⋅4=6−12=−6m/s
This means the block has a velocity of −6m/s relative to the ground after 4s.
At the moment the block comes to rest relative to the belt, its velocity relative to the ground is equal to the velocity of the belt V:
V=−6m/s
V=6m/s
The velocity of the conveyor belt V is 6m/s.
Similar Questions
In the block moves up with constant velocity v m/s. Find F

View SolutionA block slides on ice with a velocity of 5m/s comes to rest after moving through a distance of 13.5m . Find the coefficient of friction ?
View SolutionA conveyor belt is moving with constant speed of 6m/s. A small block is just dropped on it.Coefficient of friction between the two is μ=0.3. Find

(a) The time when relative motion between them will stop
(b) Displacement of block upto that instant (g=10m/s2).
View SolutionA block of mass 2 kg is moving with a velocity of 2ˆi−ˆj+3ˆk m/s. Find the magnitude and direction of momentum of the block with the x-axis.
View SolutionA particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.
View SolutionA block is gently placed on a conveyor belt moving horizontally with constant speed. After t = 4s, the velocity of the block becomes equal to the velocity of the belt. If the coefficient of friction between the block and the belt is μ=0.2, then the velocity of the conveyor belt is (g=10ms−2)
View SolutionA car A moves with velocity 15ms−1 and B with velocity 20ms−1 are moving in opposite directions as shown in . Find the relative velocity of B w.r.t. A and w.r.t. B.
 .
.
View SolutionA conveyor belt is moving at a constant speed of 2m/s . A box is gently dropped on it. The coefficient of friction between them is μ=0.5 . The distance that the box will move relative to belt before coming to rest on it taking g=10ms−2 is:
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
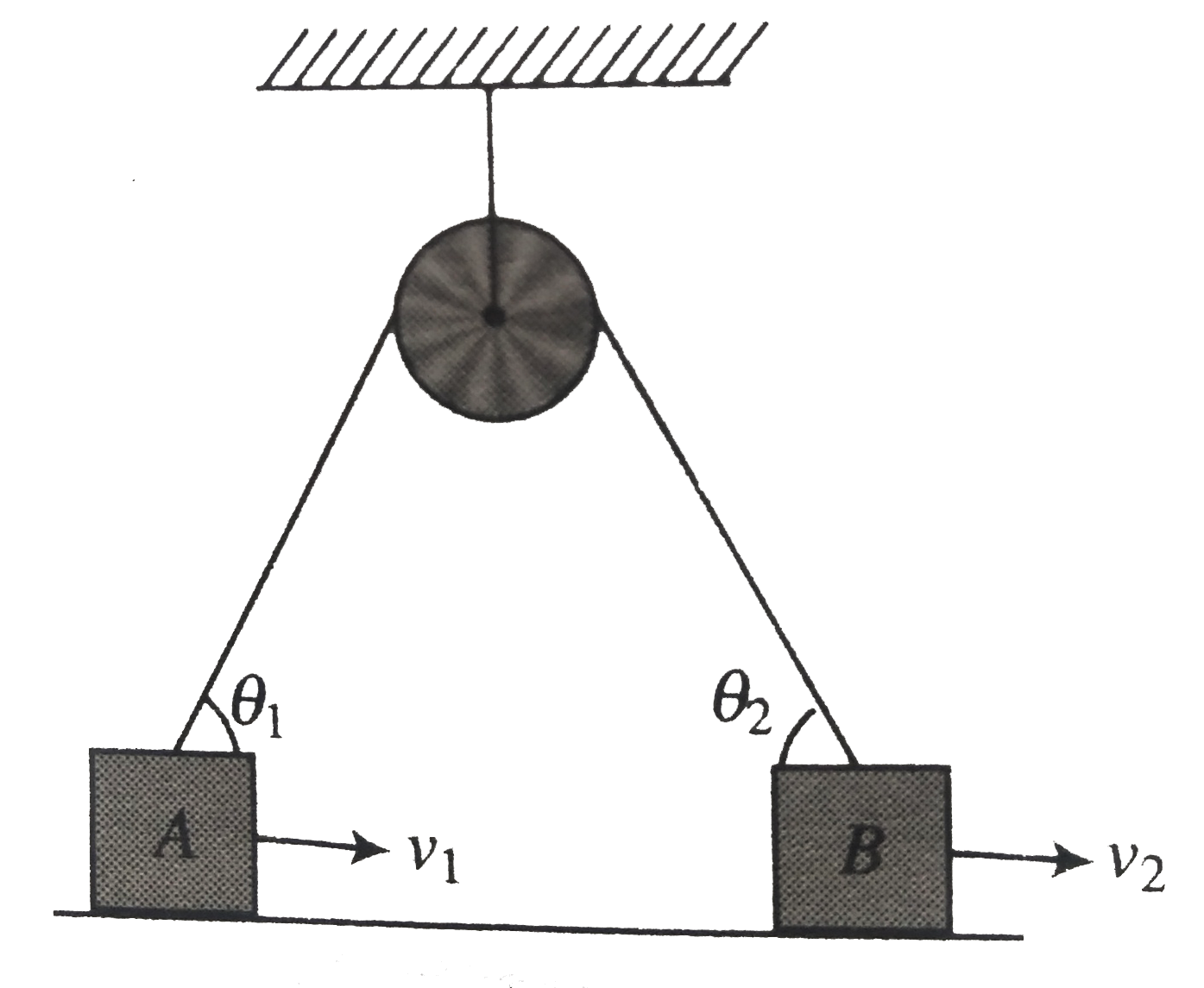
View SolutionA long conveyer belt moves with a constant velocity of 8ms−1.Two blockA and B each of mass 2kg are placed gently on the belt with B on A, initail velocity of block is zero Coefficient of friction between A and belt is 0.1 There is no friction between A and B length of A is 4m

Find the velocity of A when B falls off A
View Solution

