A monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight .The monkey move downward with respect to the rope with an acceleration b.

The acceleration of weight is
i) If the monkey is at rest on the rope, then acceleration of both mass M and monkey are same, equal to a (say)
If T is tension in the rope, then the equation of motion of monkey is
mg−T=ma1..........(1)
and equation of motion of mass M is
T=Ma1 ........... (2)
Adding (1) and (2) mg=(M+m)a1
∴a1=mM+mg ......... (3)
ii) When monkey moves upward with acceleration β, the reaction m β acts downward, therefore equations of motion now take the form (a2 is acceleration of mass, M relative to plate)
mg+mβ−T=ma2 ( for monkey ) ............. (4)
T=Ma2 ( for mass M) ............. (5)
Adding , we get , mg+mβ=(M+m)a2
∴a2=m(g+β)M+m
∴ The acceleration of mass relative to plane
a2=m(g+β)M+m ............ (6)
and acceleration of monkey M relative to plate
a2=a2−β=m(g+β)M+m−β=m(g+β)−β(M+m)M+m=mg+mβ−Mβ−mβM+m=Mg−MβM+m
iii) When monkey moves downward with acceleration β, the reaction (R=mβ) acts upward, therefore the equations of motion take the form (a3 is acceleration of block relative to plate)
mg−mβ−T=ma3 .......... (8)
T=Ma3 ............ (9)
Adding we get mg−mβ=(M+m)a3
∴a3=m(g−β)M+m
and acceleration of monkey relative to plate
a13=a3+β=m(g−β)M+m+β=mg−mβ+Mβ+mβM+m
∴a13=mg+MβM+m
Similar Questions
A monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The tension of rope is
View SolutionA cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope when the cat move upwards with in acceleration a=2m/s2 relative to the rope ?

View SolutionIf a monkey moves upward with respect to the rope with acceleration g/2 then acceleration of block, if masses of block and monkey are same
View SolutionA monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration g/4. The opposite end of the rope is tied to a block of mass M lying on a rough horizontal plane. The coefficient of friction between the block and horizontal plane is μ. Find the tension in the rope.

View SolutionA 40 kg boy climbs a rope that passes over an ideal pulley. The other end of the rope is attached to a 60 kg weight placed on the ground. What is the maximum upward acceleration the boy can have without lifting the weight ? If he climbs the rope with upward acceleration 2 g, with what acceleration the weight will rise up ?
View SolutionA weightless inextensible rope rests on a stationary wedge forming an angle α with a horizontal One end of the rope is fixed to the wall to point A.A small load is attached to the rope at point B The wedge starts moving to the right with a constant acceleration a The acceleration of the load is given by
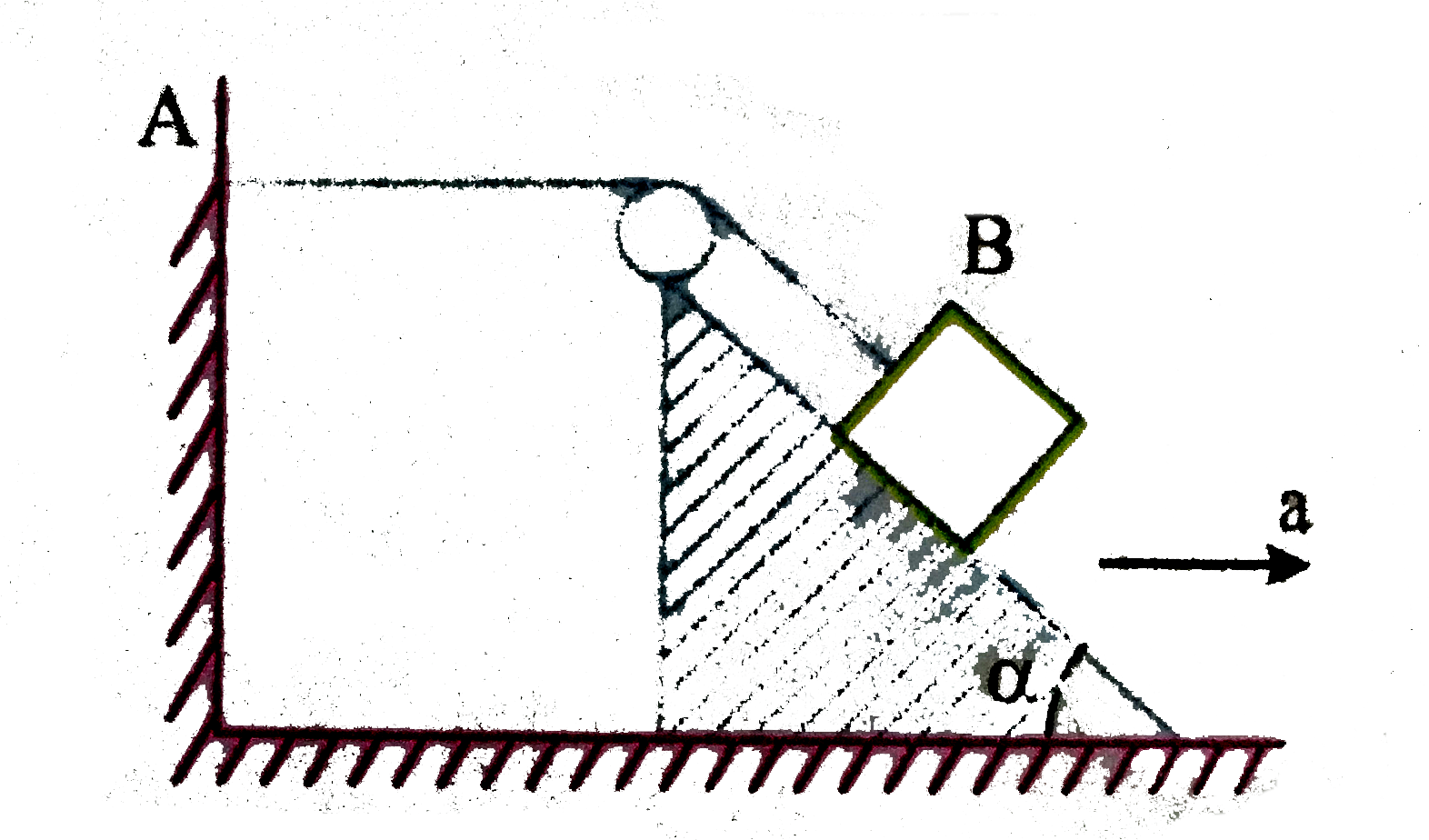 .
.
View SolutionA cart of mass M is tied to one end of a massless rope of length 10m. The other end of the rope is in the hands of a man of mass M. The entire system is on a smooth horizontal surface. The man is at x=0 and the cart at x=10m. If the man pulls the cart by the rope, the man and the cart will meet at the point
View SolutionA balloon of mass M with a light rope having monkey on the rope is in equilibrium. If the monkey starts moving up with acceleration a w.r.t. rope . Then the acceleration of cenre of mass of the system is

View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

View SolutionA block of mass 20 kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in the figure. Find the acceleration of the pulley
_PHY_E05_192_Q05.png)
View Solution
