A cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope where the cat move upwards with in acceleration a=2m/s2 relative to the rope ?

2 N
12N
8N
4N
The correct Answer is:4
→acat=(2−a) upwards =→acat/Rope+→arope
T−1g=1(2−a) …(1)
2T=2a2 … (2)
Topper's Solved these Questions
Similar Questions
A monkey of mass m climbs up to a rope hung over a fixed pulley. The opposite end of the rope is tied to a weight of mass M lying on a horizontal plane. Neglecting the friction, find the acceleration of both the bodies (relative to the plane) and the tension of the rope for the three cases:
(i) The monkey does not move with respect to the rope
(ii) The monkey moves upwards with respect to the rope with acceleration a.
(iii) The monkey moves downwards with respect to the rope, with acceleration a.
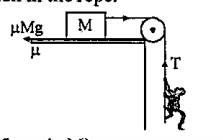
View SolutionA monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration relative to the rope g/4. The opposite end of the rope is tied to a bock of mass M lying on a rough horizontal plane. The coeffient of friction between the block and horizontal plane is μ. Find the tension in the rope
View Solution
Knowledge Check
A monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The tension of rope isAMm(μg+g+b)M+mBMm(μg−g+b)M+mCMm(μg+g−b)M+mDMm(μg−g−b)M+mA monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The acceleration of weight isA2m(g+b)−μMgM+2mBm(g+b)−μMg2(M+m)Cm(g+b)−3μMgM+3mDm(g+b)−μMgM+2mAn object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
A30.5 NB40.5 NC50.5 ND60.5 N
A monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration g/4. The opposite end of the rope is tied to a block of mass M lying on a rough horizontal plane. The coefficient of friction between the block and horizontal plane is μ. Find the tension in the rope.

View SolutionA monkey of massm clings to a rope slung over a fixed pulley. The opposite end of the rope is tied to a weight of
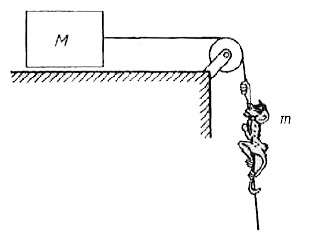
mass M lying on a horizontal plat (Fig.). Neglecting friction find the acceleration of both bodies (relative to the plate) and the tension of the rope for the three cases:
(1) the monkey does not move with respect to the rope,
(2) the monkey moves upwards with respect to the rope with acceleration b,
(3) the monkey moves downwards with respect to the rope with an acceleration b.
View SolutionA boy of mass 40kg climbs up a rope with an acceleration of 1.2ms−2.What is the tension in the rope?
View SolutionA pull of 15 N is applied to a rope attached to a block of mass 7 kg lying on a smooth horizontal surface. The mass of the rope is 0.5 kg. What is the force exerted by the block on the rope?
View SolutionTow men of masses m1andm2 hold on the opposite ends of a rope passing over a frictionless pulley. The men m1 climbs up the pore with an acceleration of 1.2m/s2 relative to the rope. The mann m2 climbs up the rope with an acceleration of 2m/s2 relative to the rope. Find the tension in the rope if m140kgandm2=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.
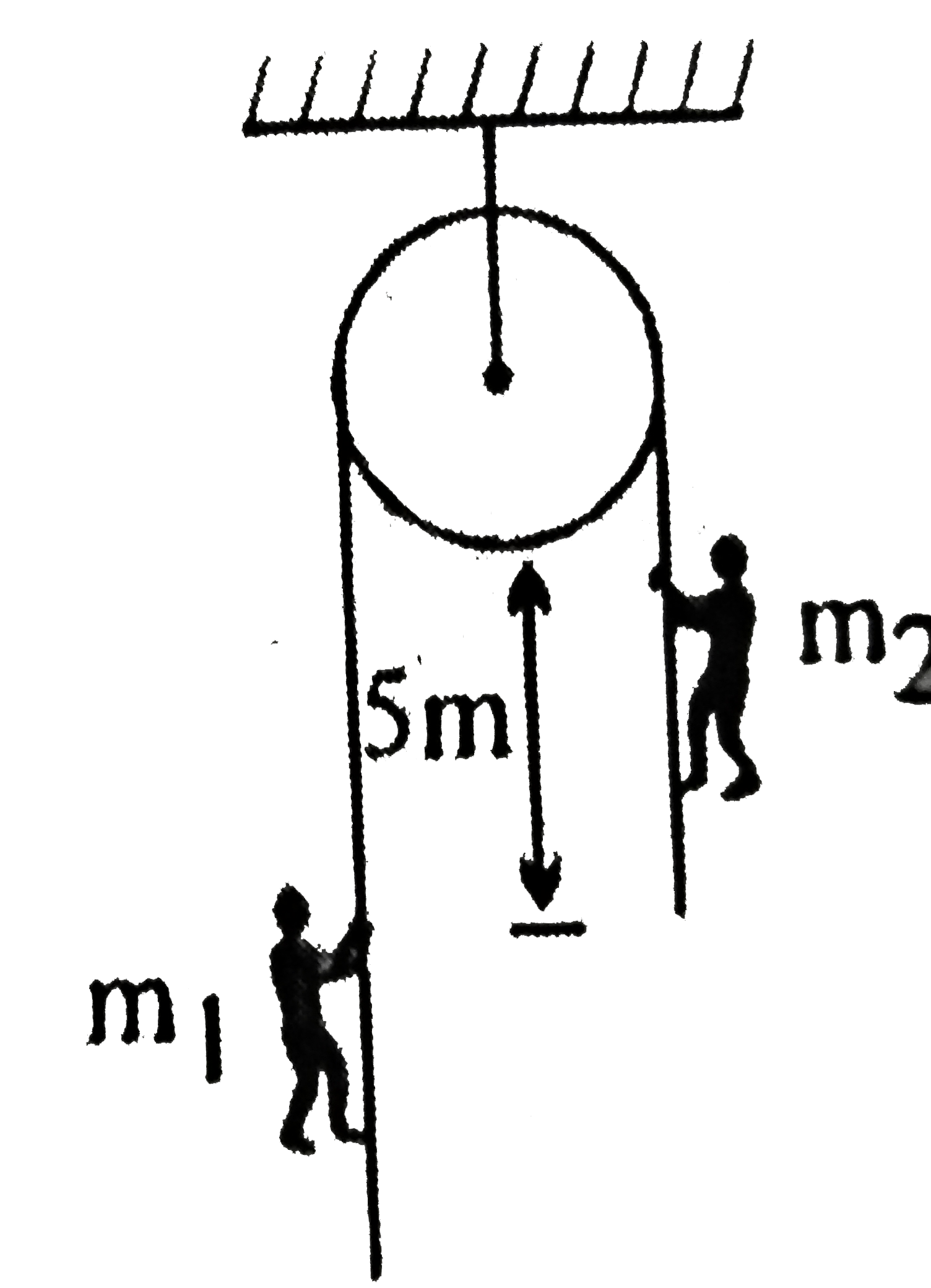
View Solution
