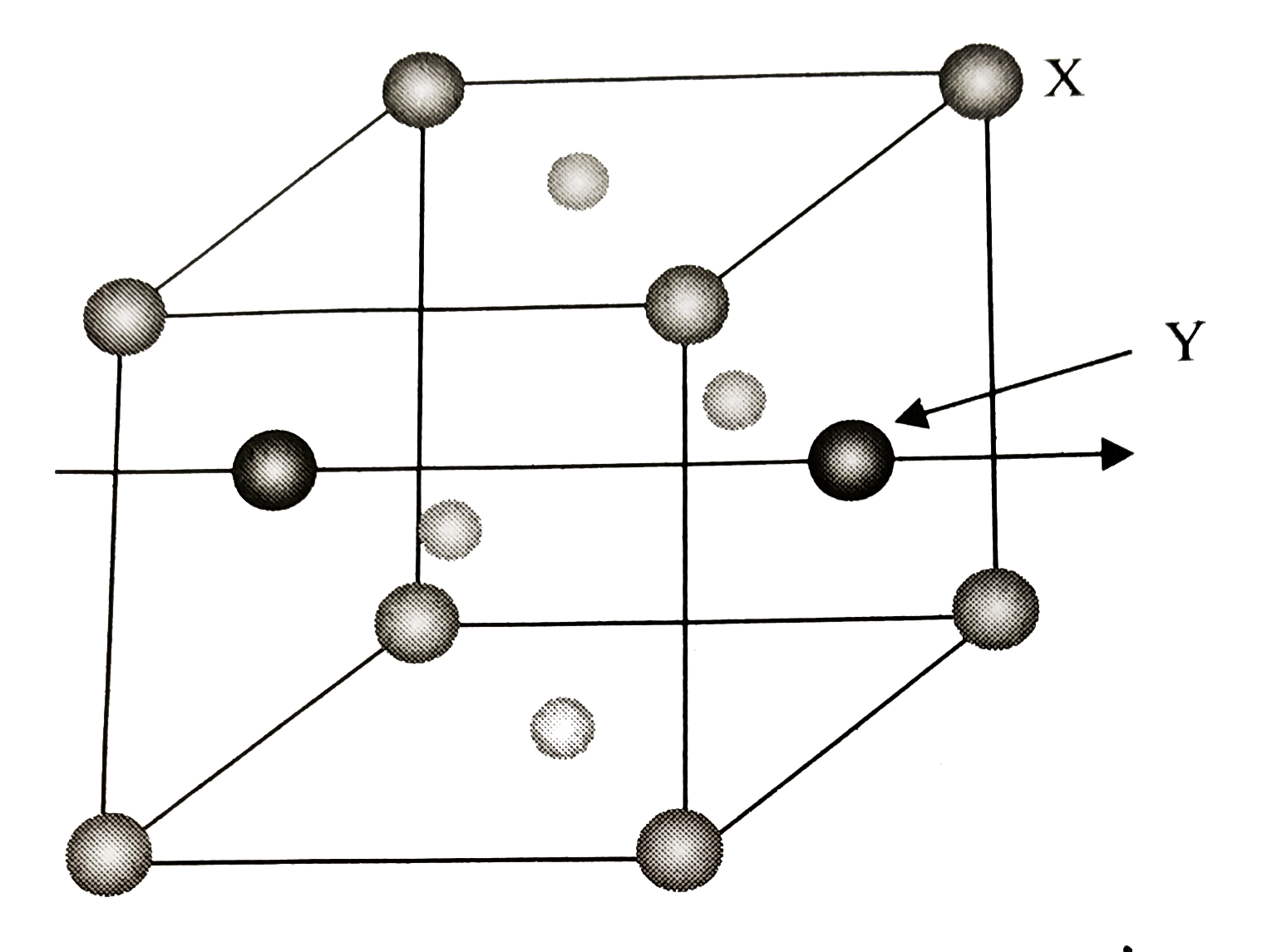
A compound formed by elements X and Y has a cubic structure in which X atoms are at the face centres. Y atoms are present at the body center and also at the alternate edge center of the cube.
a. Calculate: (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all the atoms are removed from a single axis passing through the centre of the cube, calculate
(i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.Solution in Kannada
a. i. Number of effective X atoms
=8 corners ×18 per corner atom share
=1 atom/unit cell
Number of effective Y atoms
=8 corners ×12 per face atom share
=3 atom/unit cell
Number of effective Y atoms
=8 corners ×12 per face atom share
=3 atom/unit cell
Zeff(8X+Y)=1+3=4
ii. Total atoms in a cube
=8X atoms at corner +6Y atoms at faces
=8+6=14 atoms/units cube
iii. Formula of the compound:
Zeff(x)=1,Zeff(Y)=3
Thus, formula of the compound =XY3
b. i. Two atoms from two face centres are removed by passing an axis as shown in the figure below.
∴ Face centre atom left =6−2=4
Zeff(Y)=4 Face atoms ×12 Per face atom share
=2 atoms/units cell
Zeff(X)=8 corners ×18 Per corner atom share
=1 atom/units cell
∴Zeff(X+Y)=2+1=3 atoms/units cube.
ii. Total atoms in a cube =8(corners)+4(Face centre)
=12 atoms/units cube
iii. Formula of the compound:
Zeff(X)=1,Zeff(Y)=2
∴ Formula =XY2
Similar Questions
A compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube. If all the atoms from the diagonals of one of the face of the cube are removed, then Z_(eff) is
View SolutionA compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube. If all the atoms are removed from one of the plane passing through the middle of the cube, calculate total number of atoms in the cube,
View SolutionA compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube.
If all the atoms are removed from one of the axis passing through one of the face centers of the cube, then formula of the compound is
View Solutionएक घनीय संरचना युक्त यौगिक में तत्व A के परमाणु घन के सभी कोनों पर तथा तत्व B के परमाणु घन के सभी फलकों के केंद्र पर स्थित हैं, तो यौगिक का सूत्र बताइए।
View SolutionA compound formed by elements X, Y and Z has a cubic structure in which X atoms are at the corner of the cube and also at alternate face centres. Y atoms are present at the body centre and Z atoms are present at the alternate edge centre. Then the molecular formula of the compound is
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corners of the cube of and two atoms (Y) are at each body diagonal of the cube.
a. Calculate: (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all atoms form one body diagonal of the cube except corners are removed, calculate: (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and Y atoms are at the face centres. One atoms X is misssing from the corner. a. Calculate (i). Z_(eff') (ii). total number of the atoms in the cube, and (iii). formula of the compound. b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) Z_(eff') (ii) total number of atoms in a cube, and (iii) formula of the compound.
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body centre and at the edge centre of the cube. a. Celculate (i) Z_(eff') (ii) total number of atoms in the cube, and (iii) formula of the compound. b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) Z_(eff') (ii) total number of atoms in the cube, and (iii) formula of the compound. c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) Z_(eff') (ii) total number of atoms in the cube, and (iii) formula of the compound. d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) Z_(eff') (ii) total number of atoms in the cube, and (iii) formula of the compound. e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) Z_(eff') (ii) total number of atoms in the cube, and (iii) formula of the compound.
View Solution
