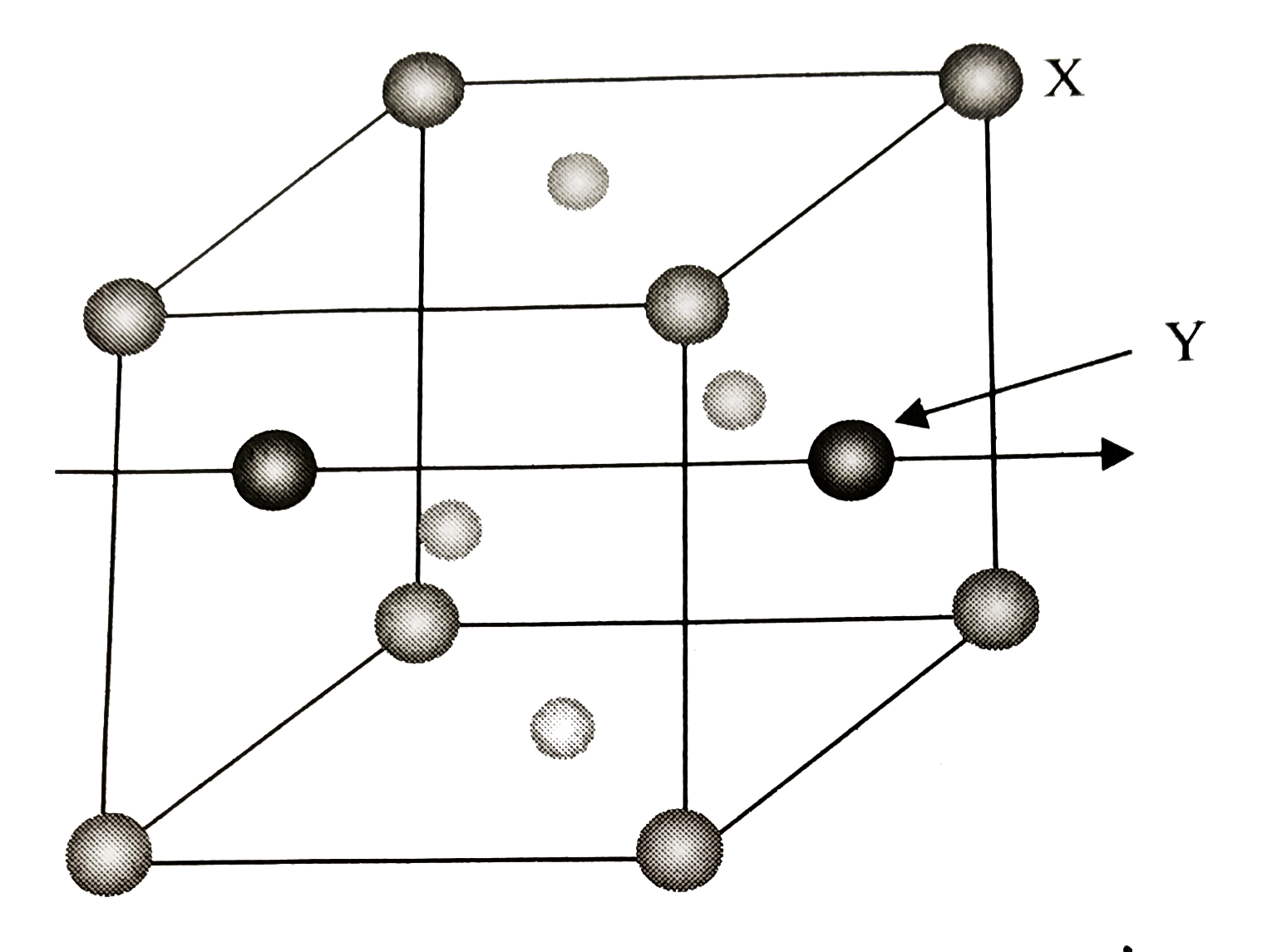
A compound formed by elements X and Y has a cubic structure in which X atoms are at the face centres.
a. Calculate: (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all the atoms are removed from a single axis passing through the centre of the cube, calculate
(i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
a. i. Number of effective X atoms
=8 corners ×18 per corner atom share
=1 atom/unit cell
Number of effective Y atoms
=8 corners ×12 per face atom share
=3 atom/unit cell
Number of effective Y atoms
=8 corners ×12 per face atom share
=3 atom/unit cell
Zeff(8X+Y)=1+3=4
ii. Total atoms in a cube
=8X atoms at corner +6Y atoms at faces
=8+6=14 atoms/units cube
iii. Formula of the compound:
Zeff(x)=1,Zeff(Y)=3
Thus, formula of the compound =XY3
b. i. Two atoms from two face centres are removed by passing an axis as shown in the figure below.
∴ Face centre atom left =6−2=4
Zeff(Y)=4 Face atoms ×12 Per face atom share
=2 atoms/units cell
Zeff(X)=8 corners ×18 Per corner atom share
=1 atom/units cell
∴Zeff(X+Y)=2+1=3 atoms/units cube.
ii. Total atoms in a cube =8(corners)+4(Face centre)
=12 atoms/units cube
iii. Formula of the compound:
Zeff(X)=1,Zeff(Y)=2
∴ Formula =XY2
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Solved Examples
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
3 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRYCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
A compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body centre and at the edge centre of the cube.
a. Celculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at alternate face entres. Y atoms are present at the body centre and also at the alternate edge centre of the cube.
a. Calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the plane passing through the middle of the cube of the cube which contains atoms both on the edge entre as well as on the face centre, calculate (i) Zeff' (ii) total number of atoms in the cube, (iii) formula of the compound.
c. If all the atoms are removed from the plane passing through the middle of the cube which contains atoms only on the edge centre but not on face centre, calculate (i) Zeff' (ii) total number of atoms in t he cube, and (iii) fomula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of the cube which neither contains atoms on the edge centre nor on the face centre, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from on e of the axes passing through the middle of the cube containing face centre atoms, calculate (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
f. If all the atoms are remove from one of the axes passing through the middle of the cube nor containing face centre atoms, calculate (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
View Solution
Knowledge Check
A compound formed by element A and B crystallizes in the cubic structure where B atoms are atg the face-centres. The formula of the compound is
AAB3BABCA3BDA2B2A compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube.
If all the atoms are removed from one of the plane passing through the middle of the cube, calculate total number of atoms in the cube,A8B9C12D18A compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube.
If all the atoms are removed from one of the axis passing through one of the face centers of the cube, then formula of the compound isAXYBXY2CX2YDXY3
A compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and Y atoms are at the face centres. One atoms X is misssing from the corner.
a. Calculate (i). Zeff' (ii). total number of the atoms in the cube, and (iii). formula of the compound.
b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
View SolutionA compound formed by elements X and Y has a cubic structure in which X atoms are at the corners of the cube of and two atoms (Y) are at each body diagonal of the cube.
a. Calculate: (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all atoms form one body diagonal of the cube except corners are removed, calculate: (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
View SolutionA compound formed by elements A and B has a cubic structure in which A atoms are at the corner of the cube and B atoms are at the face centres. Derive the fomula of the compound.
View SolutionA compound formed by elements A and B has a cubic structure in which A atoms are at the corners of the cube and B atoms are at the face centres. The formula of the compound will be
View SolutionA compound formed by elements X and Y crystallises in a cubic structure in which atoms X are at the corners of the cube and atoms Y are at two non - adjacent face - centres. The formula of the compound is
View Solution
