Select the correct option from the given alternatives.20 metres of wire is available for fancing off a flower-bed in the form of a circular sector of radius 5 metres,then the maximum area (in sq.m) of the flower bed isSolution in Marathi
15
20
25
30
The correct Answer is:C
Step by step video & text solution for Select the correct option from the given alternatives.20 metres of wire is available for fancing off a flower-bed in the form of a circular sector of radius 5 metres,then the maximum area (in sq.m) of the flower bed is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The maximum area (in sq m) of a flower bed is if there is a 20 m wire available for siege of a flower bed, which is in the form of a sector of a vow.
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्य खंड के रूप में है, की घेराबंदी करने के लिये बीस मीटर तार उपलब्ध है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल ( वर्ग मी. में ) है
View SolutionTwenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: 25 (2) 30 (3) 12.5 (4) 10
View SolutionA wire of length 20m is available to fence off a flower bed in the form of a sector of a circle. What must be the radius of the circle, if we wish to have a flower bed with the greatest possible area?
View SolutionTwenty metres are available to fence a flower bed in the form of a circular sector. If the flower bed should have the greatest possible surface area, the radius of the circle must be
View SolutionTwenty two meters are available to fence a flower bed in the form of a circular sector. If the flower bed should have the greatest possible surface area, the radius of the circle must be:
View SolutionTwenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: (a) 25 (2) 30 (3) 12.5 (4) 10
View SolutionThe adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find: the area of the flower bed
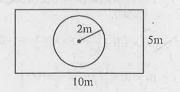
View Solution
