Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: (a) 25 (2) 30 (3) 12.5 (4) 10Solution in Tamil
30
12.5
10
25
The correct Answer is:4
Total length r+r+rθ=2θ
→θ=20−2rr ltbvrgt Therefore area of flower bed

A=12r2θ=12r220−2rr
→A=10r−r2=25−(r−5)2
∴Amax=25 (when r=5)
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - JEE Advanced Previous Year
17 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Numerical)
20 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
13 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
The function f:[0,3]−−−→1,29, defined by f(x)=2x3−15x2+36x+1, is one-one and onto onto but not one-one one-one but not onto neither one-one nor onto
View SolutionIf α is an integer satisfying |α|≤4−|[x]|, where x is a real number for which 2xtan−1x is greater than or equal to ln(1+x2), then the number of maximum possible values of a (where [.] represents the greatest integer function) is_____
View SolutionLet f:(−5,5)→R be a differentiable function with f(4) = 1, f′(4)=1,f(0)=−1 and f^(')(0) = 1,Ifg(x) = f(2f^(2)(x)+2))^(2),then - g^(')(0) equals
View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?
View SolutionA circular flower bed is surrounded by a path 4m wide. The diameter of the flower bed is 66m. What is the area of this path ? (π=3.14)
View SolutionTwenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: 25 (2) 30 (3) 12.5 (4) 10
View SolutionTwenty meters of wire is available for fencing a flower -bed in the form of a circular sector .Then the maximum area in square meters of the flower bed is
View Solutionएक सेक्टर के रूप में बनी फूलों की एक क्यारी पर 40 मी लम्बाई के एक तार से बाड़ लगाई गयी है । यदि क्यारी का अधिकतम सम्भावित क्षेत्रफल हो, तो सेकण्ड की त्रिज्या क्या है ?
View SolutionTwenty meters of wire is available to fence off a flower bed in the form of a sector. If the flower bed has the maximum surface then radius is
View SolutionTwenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: (1) 25 (2) 30 (3) 12.5 (4) 10
View SolutionThe maximum area (in sq m) of a flower bed is if there is a 20 m wire available for siege of a flower bed, which is in the form of a sector of a vow.
View SolutionThe maximum area (in sq m) of a flower bed is if there is a 20 m wire available for siege of a flower bed, which is in the form of a sector of a vow.
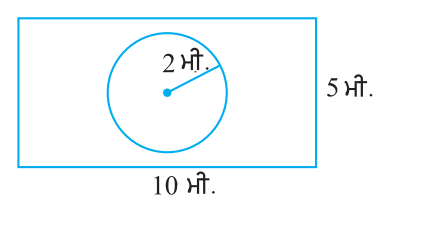
View Solutionਜਿਵੇਂ ਚਿਤਰ ਵਿਚ ਵਿਖਾਇਆ ਗਿਆ ਹੈ, ਇੱਕ ਆਇਤਕਾਰ ਪਾਰਕ ਦੇ ਕੇਂਦਰ ਵਿੱਚ ਇਕ ਚੱਕਰਾਕਾਰ ਫੁੱਲਾਂ ਦੀ ਕਿਆਰੀ ਹੈ। ਪਤਾ ਕਰੋ:- ਫੁੱਲਾਂ ਦੀ ਕਿਆਰੀ ਨੂੰ ਛੱਡ ਕੇ, ਪਾਰਕ ਦੇ ਬਾਕੀ ਭਾਗ ਦਾ ਖੇਤਰਫਲ
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्य खंड के रूप में है, की घेराबंदी करने के लिये बीस मीटर तार उपलब्ध है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल ( वर्ग मी. में ) है
View SolutionTwenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: 25 (2) 30 (3) 12.5 (4) 10
View Solution
