Twenty metres of wire is available for fencing off a flower-bed in the form of a circular sector. Then the maximum area (in sq.m) of the flower-bed is: (1) 25 (2) 30 (3) 12.5 (4) 10
To find the maximum area of a flower-bed in the form of a circular sector using 20 meters of wire, we can follow these steps:
Step 1: Understand the problem
We have a circular sector with a radius r and a central angle θ. The total length of the wire used for fencing is 20 meters. The fencing consists of the arc length and the two straight sides (radii).
Step 2: Set up the equation for the wire length
The length of the wire used can be expressed as:
Arc length+Two radii=20
The arc length of the circular sector is given by rθ. Therefore, we can write:
rθ+2r=20
Step 3: Rearrange the equation
We can rearrange this equation to express θ in terms of r:
rθ=20−2r
θ=20−2rr
Step 4: Write the area of the circular sector
The area A of a circular sector is given by:
A=12r2θ
Substituting the expression for θ:
A=12r2(20−2rr)
This simplifies to:
A=12r(20−2r)
A=10r−r2
Step 5: Differentiate the area function
To find the maximum area, we differentiate A with respect to r:
dAdr=10−2r
Step 6: Set the derivative to zero
Setting the derivative equal to zero to find critical points:
10−2r=0
2r=10⟹r=5
Step 7: Verify that it is a maximum
To confirm that this critical point is a maximum, we can check the second derivative:
d2Adr2=−2
Since the second derivative is negative, r=5 gives a maximum area.
Step 8: Calculate the maximum area
Now we substitute r=5 back into the area formula:
A=10(5)−(5)2
A=50−25=25
Conclusion
The maximum area of the flower-bed is 25sq m.
We have a circular sector with a radius r and a central angle θ. The total length of the wire used for fencing is 20 meters. The fencing consists of the arc length and the two straight sides (radii).
The length of the wire used can be expressed as:
Arc length+Two radii=20
The arc length of the circular sector is given by rθ. Therefore, we can write:
rθ+2r=20
We can rearrange this equation to express θ in terms of r:
rθ=20−2r
θ=20−2rr
The area A of a circular sector is given by:
A=12r2θ
Substituting the expression for θ:
A=12r2(20−2rr)
This simplifies to:
A=12r(20−2r)
A=10r−r2
To find the maximum area, we differentiate A with respect to r:
dAdr=10−2r
Setting the derivative equal to zero to find critical points:
10−2r=0
2r=10⟹r=5
To confirm that this critical point is a maximum, we can check the second derivative:
d2Adr2=−2
Since the second derivative is negative, r=5 gives a maximum area.
Now we substitute r=5 back into the area formula:
A=10(5)−(5)2
A=50−25=25
The maximum area of the flower-bed is 25sq m.
Topper's Solved these Questions
Similar Questions
A wire of length 20m is available to fence off a flower bed in the form of a sector of a circle. What must be the radius of the circle, if we wish to have a flower bed with the greatest possible area?
View SolutionIn Fig. 19, the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.
View SolutionFind maximum possible area that can be enclosed by a wire of length 20cm by bending it in form of a circular sector. 10 (b) 25 (c) 30 (d) 20
View SolutionIf one of the diameters of the circle, given by the equation, x2+y2−4x+6y−12=0 , is a chord of a circle S, whose centre is at (−3,2) , then the radius of S is : (1) 5√2 (2) 5√3 (3) 5 (4) 10
View SolutionThe shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn there are flower-beds having a uniform width of 2 m.
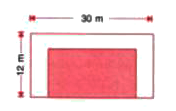
Hence, or otherwise, find the area of the flower- beds.
View SolutionMaximum possible area that can be enclosed by a wire of length 20 cm by bending it in form of a circular sector is 10 b. 25 c. 30 d. 20
View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
View SolutionIf the mid-point of a chord of the ellipse x216+y225=1 (0, 3), then length of the chord is (1) 325 (2) 16 (3) 45 12 (4) 32
View SolutionA circular flower bed is surrounded by a path 4m wide. The diameter of the flower bed is 66m. What is the area of this path ? (π=3.14)
View Solution

