Let Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+100Σk=1∣∣(k2−3k+1)Sk∣∣is ____________Solution in Kannada
Sk=a1−r=k−1k!1−1k=kk!=1(k−1)!
Now, 100∑k=2∣∣(k2−3k+1)Sk∣∣=100∑k=2∣∣∣(k2−3k+1)⋅1(k−1)!∣∣∣
=100∑k=2∣∣∣(k−1)(k−2)=k(k−1)!∣∣∣
=∣∣∣10!−21!∣∣∣+∣∣∣21!−32!∣∣∣+∣∣∣32!−43!∣∣∣+.........+∣∣∣9998!−10099!∣∣∣
=(21!−10!)+(21!−32!)+(32!−43!)+.........+(9998!−10099!)
=3−10099=3−(100)2100!
∴(100)2100!+100∑k=2∣∣(k2−3k+1)Sk∣∣=3.
Similar Questions
Let Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________
View SolutionFor k=2,3,…, let Sk denote the sum of the infinite G.P. whose first term is k2+k−2 and common ratio is 1k, then ∞Σk=1Sk2k=
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
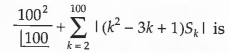 is
is
View SolutionLet Sk be the sum of an infinite G.P. series whose first term is k and common ratio is kk+1(k>0). Then the value of ∞∑k=1(−1)ksk is equal to
View SolutionFind the sum of first 100 terms of the series whose general term is given by ak=(k2+1)k!
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View Solution
