AB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If ∠ACD=32∘, then the measure of ∠AOD is .......
48∘
96∘
108∘
80∘
The correct Answer is:B
To solve the problem step by step, we will analyze the given information and apply the properties of circles and angles.
Step 1: Understand the Circle and Given Angles
We have a circle with center O, a chord AB, and a point C such that BC is equal to the radius of the circle. We are given that angle ACD = 32 degrees.
Step 2: Identify the Triangle
Since BC is equal to the radius (let's denote the radius as r), we know that OB (the radius from O to point B) is also equal to r. Therefore, triangle OBC is isosceles with OB = OC = r.
Step 3: Apply the Isosceles Triangle Property
In triangle OBC, since OB = OC, the angles opposite these sides are equal. Therefore, angle OBC = angle OCB. Let's denote these angles as x.
Step 4: Use the Angle Sum Property
The sum of angles in triangle OBC is 180 degrees:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known values:
x+x+∠BOC=180∘
This simplifies to:
2x+∠BOC=180∘
Thus,
∠BOC=180∘−2x
Step 5: Relate Angle ACD to Angle BOC
We know that angle ACD = 32 degrees. By the properties of angles in circles, angle ACD is equal to angle BOC (since they subtend the same arc AD). Therefore:
∠BOC=32∘
Step 6: Substitute Back to Find x
Now we can substitute back into our equation:
180∘−2x=32∘
Rearranging gives:
2x=180∘−32∘
2x=148∘
Thus,
x=74∘
Step 7: Find Angle AOD
Now, angle AOD is the angle at the center of the circle that subtends the same arc AD as angle ACD. By the inscribed angle theorem, angle AOD is twice angle ACD:
∠AOD=2×∠ACD=2×32∘=64∘
Step 8: Final Calculation
We have found that angle AOD measures 64 degrees.
Conclusion
The measure of angle AOD is 64 degrees.
We have a circle with center O, a chord AB, and a point C such that BC is equal to the radius of the circle. We are given that angle ACD = 32 degrees.
Since BC is equal to the radius (let's denote the radius as r), we know that OB (the radius from O to point B) is also equal to r. Therefore, triangle OBC is isosceles with OB = OC = r.
In triangle OBC, since OB = OC, the angles opposite these sides are equal. Therefore, angle OBC = angle OCB. Let's denote these angles as x.
The sum of angles in triangle OBC is 180 degrees:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known values:
x+x+∠BOC=180∘
This simplifies to:
2x+∠BOC=180∘
Thus,
∠BOC=180∘−2x
We know that angle ACD = 32 degrees. By the properties of angles in circles, angle ACD is equal to angle BOC (since they subtend the same arc AD). Therefore:
∠BOC=32∘
Now we can substitute back into our equation:
180∘−2x=32∘
Rearranging gives:
2x=180∘−32∘
2x=148∘
Thus,
x=74∘
Now, angle AOD is the angle at the center of the circle that subtends the same arc AD as angle ACD. By the inscribed angle theorem, angle AOD is twice angle ACD:
∠AOD=2×∠ACD=2×32∘=64∘
We have found that angle AOD measures 64 degrees.
The measure of angle AOD is 64 degrees.
Similar Questions
AB is the chord of a circle with centreO. AB is produced to C, such that BC =OB, CO is joined and produced to meet the circle in D.
If ∠ACD=Y∘ and ∠AOD=x∘, Prove that x=3y.
View SolutionIn the figure given below, AB is the chord of a circle with centre O. AB is extended to C such that BC = OB. The straight line Co is produced to meet the circle at D. If ACD = y and AOD = x, such that x = ky, then the value of k is.
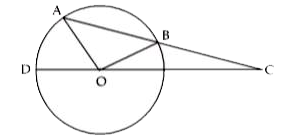
View Solution
Knowledge Check
AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If ∠BCD=20∘, then ∠AOD= ?
A20∘B30∘C40∘D60∘
In the figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
∠AOB
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of sector of the circle formed by chord AB .
View SolutionAB is a diameter of a circle with centre O. The tangents at C meets AB produced at Q. if ∠CAB=34∘, then measure of is ∠CBA is
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionAB is a chord of a circle with centre O and diameter 20 cm. If AB = 12 cm, find the distance of AB from O.
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
View Solution
