AB is a chord of a circle (centre o) and DOC is a line segment originating from a point D on the Circle and intersecting AB on Producing at C such that BC = OD. If ∠BCD=20∘, then ∠AOD :-
30∘
40∘
10∘
60∘
The correct Answer is:D
Step by step video, text & image solution for AB is a chord of a circle (centre o) and DOC is a line segment originating from a point D on the Circle and intersecting AB on Producing at C such that BC = OD. If angle BCD = 20^(@), then angle AOD :- by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If ∠BCD=20∘, then ∠AOD= ?
A20∘B30∘C40∘D60∘AB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?A5∘B7∘C17∘D6∘AB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If ∠ACD=32∘, then the measure of ∠AOD is .......
A48∘B96∘C108∘D80∘
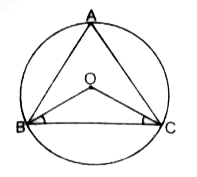
BC is a chord to a circle with centre O. A is a point on major are BC as shown in the below figure. What is the value of ∠BAC+∠OBC ?
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
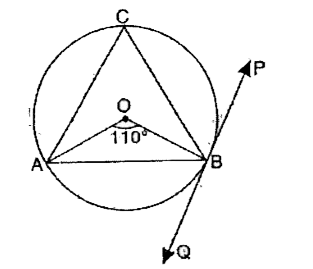
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
View SolutionTwo chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
View SolutionThe chord AB of a circle of centre O subtends an angle θ with the tangent at A to the circle. Then measure of ∠ABOis :
View Solution
