A cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 Solution in Tamil
Solution in Tamil
The portion of th strings between the cweiling and the cylinder is at rest. Hence the oints o the cuylinder where the strings leave it are at rest. The cylinder is thus rolling withuot sliping on the strings. Suppose the centre of the cylinder falls with n acceleration a. The ngular acceleration of he cylenere about its axis s α=aR, as the cylinder does not slip ovr teh strings.
The equation of motion for the centre of mass of the cylinder is
mg-2T=ma.............i<br>andforthemotionaboutthecentreofmassitas<br>2Tr=(1/2mr^2alpha)=1/2mra<br>or2T=1/2ma............ii<br>Fromiandii<br>a=2/3g and T=(mg)/6<br>Asthecentreofthecyl∈der⋆tsmov∈gomrest,tehvelocityafterithsfal≤nthroughadistancehisgivenby<br>v^2=2(2/3g)h<br>orv=(sqrt(4gh))/3
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
Can an object be in pure translation as well as in pure rotation?
View SolutionLet →A be a unit vector along the axis of rotation of a purely rotating body and →B be a unit vector along the velocity of a particle P of the body away from the axis. The value of →A.→B is
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA string of negligible thicknes is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the sitting an pulls the cylinder towards him figure. There is no slipping anywhere. The length of the string passed through the hand of the man whicle the cylinder reaches his hands is

View SolutionConsider the arrangement shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a masslessm frictionless pulley to a falling weight, determine the acceleration of the falling mass m in terms of only the mass of the cylinder M , the mass m and g
View Solution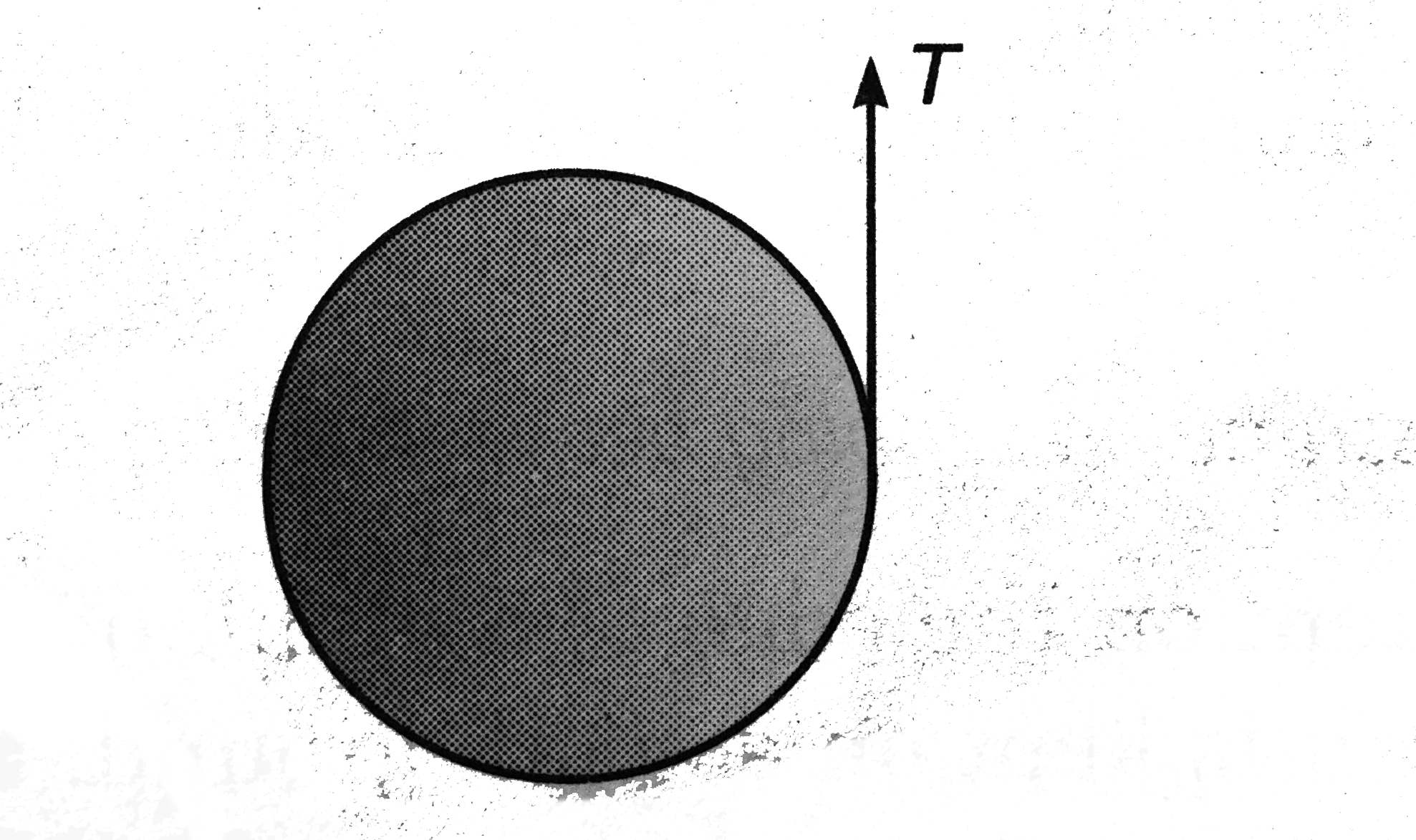
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA string is wrapped around a cylinder of mass M and radius R . The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA solid cylinder has a thin string wrapped several times around its circumference. The string is fixed at one end and the cylinder is released. Find the downward acceleration of cylinder and tension in the string.
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed omega .
View SolutionA string is wrapped around a cylinder of mass M and radius r. The string is pulled vertically upward to prevent the center of mass from falling as the cylinder unwinds the string. (a) What is the tension in the string? B) How much work has been done on the cylinder once it has reached an angular speed omega ? c) what is the length of string unwound in the time its acquires angular speed omega ?
View SolutionA cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate (a) The downward linear acceleration of the cylinder (b) The tension in the strings (c) The time dependence of the instantaneous power developed by gravity
View SolutionA string is wrapped around a cylinder of mass M and radius R(=2√2m).The string is pulled vertically upward to prevent the centre of mass from falling as the cylinder unwinds the string.Find the length of the string unwound when the cylinder has reached a speed ω(=5rad/s).(g=10ms2)
View SolutionA string of negligible thicknes is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the sitting an pulls the cylinder towards him figure. There is no slipping anywhere. The length of the string passed through the hand of the man whicle the cylinder reaches his hands is

View Solution
