A bullet of mass 10g moving horizontally at a speed of 50
7
m/s strikes a block of mass 490g kept on a frictionless track as shown in figure. The bullet. remains inside the block and the system proceeds towards the semicircular track of radius 0.2m. Where will the block strike the horizontal part after leaving the semicircular track?
 Solution in Tamil
Solution in Tamil
mass of block =490 gm
mss of bullet = 10gm
Since the bullet embedded inside the block, it is a plastic collision
Initial velocity of bullet
v1=50√7ms
velocity of the block is v2=0
Let fiN/Al velocity of boty =v
Hence 10×10−350√7+490×10−3×0
(490+10)
=10−3×VA
∴VA=√7ms ltbr> When the block loses the contat at D the component mg will act on it,
m(VB)2r=mgsinθ
→(VB)2=grsinθ .........i
puting work energy principle
(12)m×(VB)2−(12)×m×(VA)2
=−mg(0.2+0.2sinθ)
→(12)×grsintehta−(12)×(√7)2
=g(0.2+0.2sinθ)
→3.5−(12)+9.8+0.2+sinθ
=9.8+0.2(1+sinθ)
rarr 3.5-0.98sinthea=1.96+1.96sintheta<br>rarr sintheta=(1/2)<br>rarr theta=30^0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C09_E01_109_S01.pngwh=80%mx-autosty≤=background:white;><br>:. Angle of projection =900−300=600
∴ time of reaching the ground =(√2hg)
,=⎛⎝√2x0.2+0.2×sin3009.8=0.247sec
→Distancetravel≤d∈horizontaldirection<br>S=vcos q xxt<br>=sqrt(grsintheta) cos thetaxxt <br>=sqrt(9.8xx2xx(1/2)sqrt3/2xx0.247<br>0.196m<br>Totaldistance=(0.2-0.2cos30^0+0.196)<br>=0.22m
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
View SolutionA bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View SolutionAOB is a smooth semicircular track of radius r. A block of mass m is given a velocity √2rg parallel to track at point A. Calculate normal reaction between block and track when block reaches at point O.

View SolutionThe length of ballistic pendulum is 1m and mass of its block is 0.98kg. A bullet of mass 20 gram strikes the block along horizontal direction and gets embedded in the block. If block + bullet completes vertical circle of radius 1m, then the striking velocity of bullet is
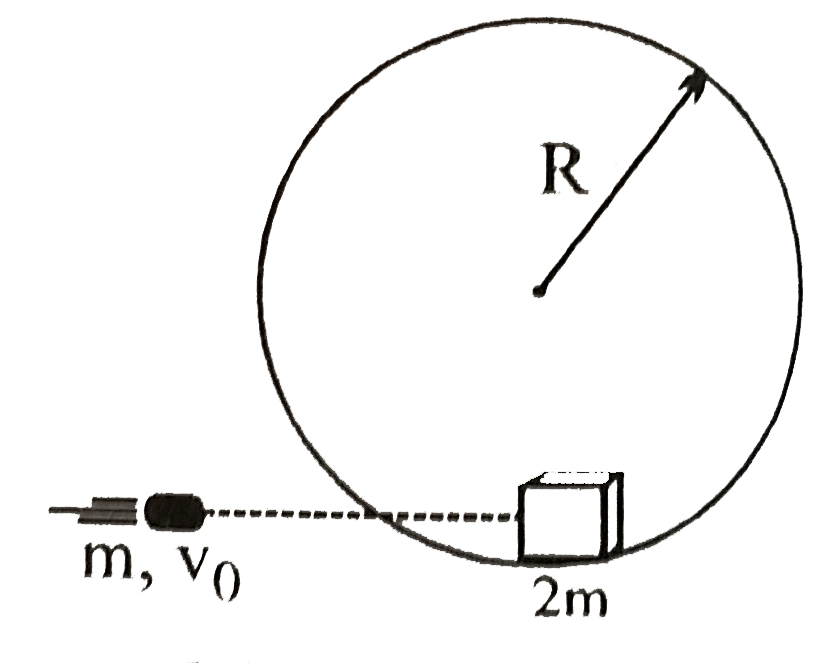
View SolutionA small block of mass 2m initially rests at the bottom of a fixed circular, vertical track, which has a radius of R. The contact surface between the mass and the loop is frictionless. A bullet of mass m strikes the block horizontally with initial speed v0 and remain embedded in the block as the block and the bullect circle the loop. Determine each of the following in terms of m,R and g.
(a) The speed of the masses immediately after the impact.
(b) The minimum initial speed of the bullet if the block and the bullet are to successfully execute a complete ride on the loop
View SolutionA wooden block of mass M rests on a horizontal surface. A bullet of mass m moving in the horizontal direction strikes and gets embedded in it. The combined system covers a distance x on the surface. If the coefficient of friction between wood and the surface is mu , the speed of the bullet at the time of striking the block is (where m is mass of the bullet)
View Solutionv चाल से चलती हुई द्रव्यमान की एक गोली m द्रव्यमान के स्थिर ब्लॉक से टकराती है। ब्लॉक से m' द्रव्यमान का एक छोटा टुकड़ा अलग होकर गोली से चिपक जाता है। शेष ब्लॉक v1 चाल से गोली की दिशा में गतिशील हो जाता है। टक्कर के पश्चात गोली का वेग ज्ञात करें।
View Solutionक्षैतिज दिशा में 50√7m/s चाल से गतशील 10g द्रव्यमान वाली तंदक की एक गोली, चित्र 15.E8 में दिखाई गई घर्षणरहित सतह पर स्थित 490g द्रव्यमान के गुटक से टकराती है। गोली, गुटके में फँसी रहे जाती है तथा यह गुटका 0.2 m त्रिज्या वाले अर्द्धवृत्ताकार पथ की ओर चलने लगता है। अद्धवृत्ताकार पथ को छोड़ने पश्चात गुटका क्षैतिज पथ पर कहा टकराएगा

View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View SolutionA bullet of mass 50 g , moving a velocity of 200 m*s^(-1) , strikes and penetrates a wooden block. If the resistance f the wooden block on the bullet is 4900 N, find the distance up to which the bullet penetrates the block.
View SolutionA bullet of mass 'm' moving with velocity *v' strikes a block of mass 'M' at rest and gets embeded into it. The K.E. of composite block will be:
View SolutionA block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View SolutionA 2.0-kg pistol fires a 1.0-g bullet with a muzzle speed of 1000 m/s. The bullet then strikes a 10-kg wooden block resting on a horizontal frictionless surface. The block and the embedded bullet then slide across the surface.

What is the speed of the "bullet + block" system immediately after the bullet is embedded in the block?
View Solution10g ভরের একটি বুলেট 150 m / s বেগে অনুভূমিক দিকে গতিশীল হয়ে একটি স্থির কাঠের ব্লককে আঘাত করে 0.03 s- এ স্থির হল । বুলেটটি কাঠের মধ্যে কতটা দূরত্ব ভেদ করবে ? কাঠের ব্লকটি বুলেটের ওপর কতটা বল প্রয়ােগ করবে ?
View Solution
