A bullet of mass 5gm is fired horizontally into block of mass 1kg at rest on a horizontal surface and gets embedded in it. The combination moves 5m before coming to rest. If μk=0.40, what is the speed with which the bullet strikes the block ?
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a bullet of mass mb=5g=0.005kg that is fired horizontally into a block of mass mB=1kg at rest. After the bullet embeds itself in the block, they move together and come to rest after traveling a distance of d=5m. The coefficient of kinetic friction between the block and the surface is μk=0.40. We need to find the speed v with which the bullet strikes the block.
Step 2: Use Conservation of Momentum
When the bullet embeds itself in the block, we can apply the conservation of momentum:
mbv=(mb+mB)v′
Here, v′ is the velocity of the combined system (bullet + block) immediately after the collision.
Step 3: Calculate the Velocity After Collision
The mass of the bullet is negligible compared to the mass of the block, so we can approximate:
v′≈mbvmB
Step 4: Use Work-Energy Principle
The work done by friction as the block moves a distance d is equal to the initial kinetic energy of the system just after the collision:
Work done by friction=μk(mb+mB)gd
The initial kinetic energy of the system is:
K.E.=12(mb+mB)v′2
Setting these equal gives us:
μk(mb+mB)gd=12(mb+mB)v′2
Step 5: Simplify the Equation
We can cancel (mb+mB) from both sides (since it's non-zero):
μkgd=12v′2
Step 6: Solve for v′
Rearranging gives:
v′2=2μkgd
Taking the square root:
v′=√2μkgd
Step 7: Substitute Values
Now, substituting μk=0.40, g=10m/s2, and d=5m:
v′=√2⋅0.40⋅10⋅5
Calculating this gives:
v′=√40=2√10m/s
Step 8: Substitute Back to Find v
Now we can substitute v′ back into the momentum equation to find v:
v=(mb+mB)v′mb=(0.005+1)⋅2√100.005
Calculating this gives:
v≈400√10m/s
Final Answer
Thus, the speed with which the bullet strikes the block is approximately 400√10m/s.
---
We have a bullet of mass mb=5g=0.005kg that is fired horizontally into a block of mass mB=1kg at rest. After the bullet embeds itself in the block, they move together and come to rest after traveling a distance of d=5m. The coefficient of kinetic friction between the block and the surface is μk=0.40. We need to find the speed v with which the bullet strikes the block.
When the bullet embeds itself in the block, we can apply the conservation of momentum:
The mass of the bullet is negligible compared to the mass of the block, so we can approximate:
The work done by friction as the block moves a distance d is equal to the initial kinetic energy of the system just after the collision:
We can cancel (mb+mB) from both sides (since it's non-zero):
Rearranging gives:
Now, substituting μk=0.40, g=10m/s2, and d=5m:
Now we can substitute v′ back into the momentum equation to find v:
Thus, the speed with which the bullet strikes the block is approximately 400√10m/s.
Topper's Solved these Questions
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Additional solved examples
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Conceptual short answer questions with answer
9 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
Similar Questions
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass 25 g is fired horizontally into a ballistic pendulum of mas 5.0 kg and gets embedded in it figure. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA bullet of mass 10 g is fired horizontally into a 4 kg wooden block resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet is embadded the block and the combination moves a distance of 20 m before coming to rest. Find the speed of the bullet just before striking the block. (g=10m/s2)
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
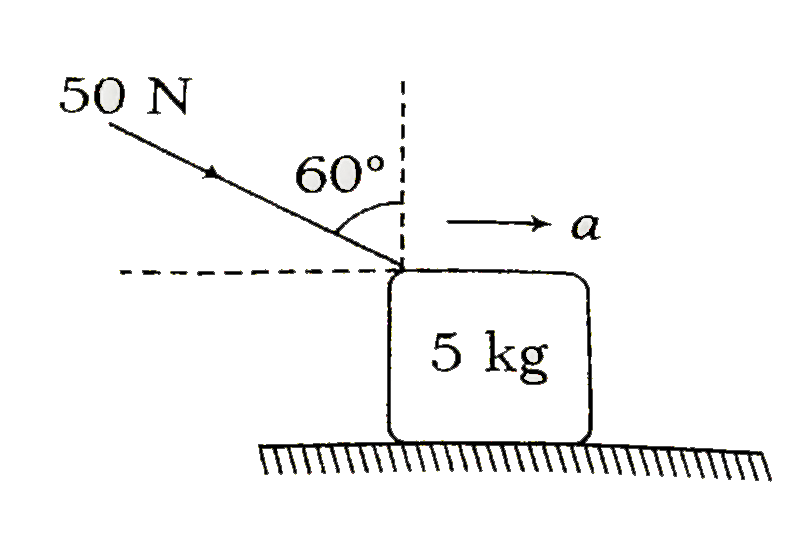
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.

View SolutionA block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
View Solution
